| Window Reference |
Factored ARIMA Model Specification Window
Use the ARIMA Model Specification window to specify an ARIMA model by using the notation:
p = (lag, ..., lag) ...(lag, ..., lag) d = (lag, ..., lag) q = (lag, ..., lag) ...(lag, ..., lag)
where p, d, and q represent autoregressive, differencing, and moving-average terms, respectively.
Access it from the Develop Models menu, where it is invoked from the Fit Model item under Edit in the menu bar, or from the pop-up menu when you click an empty area of the model table.
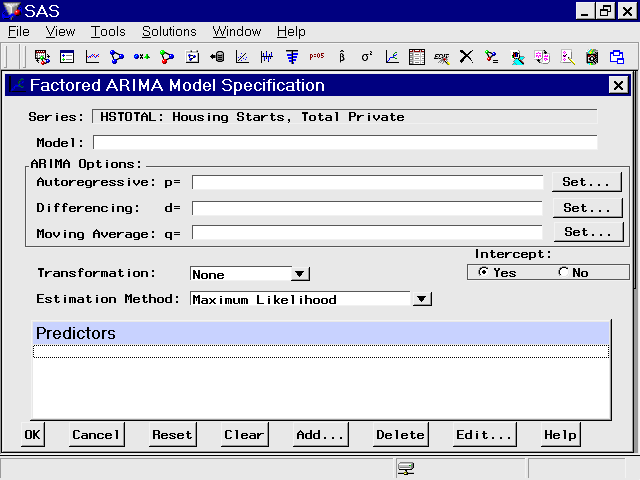
The Factored ARIMA Model Specification window is identical to the ARIMA Model Specification window, except that the p, d, and q terms are specified in a more general and less limited way. Only those controls and fields that differ from the ARIMA Model Specification window are described here.
Controls and Fields
- Model
is a descriptive label for the model. You can type a label in this field or allow the system to provide a label. If you leave the label blank, a label is generated automatically based on the p, d, and q terms that you specify. For example, if you specify p=(1,2,3), d=(1), q=(12) and no intercept, the model label is ARIMA p=(1,2,3) d=(1) q=(12) NOINT. For monthly data, this is equivalent to the model ARIMA(3,1,0)(0,0,1)s NOINT as specified in the ARIMA Model Specification window or the Custom Model Specification window.- ARIMA Options
Specifies the ARIMA model in terms of the autoregressive lags (p), differencing lags (d), and moving-average lags (q).- Autoregressive
defines the autoregressive part of the model. Select the Set button to open the AR Polynomial Specification window, where you can add any set of autoregressive lags grouped into any number of factors.- Differencing
specifies differencing to be applied to the input data. Select the Set button to open the Differencing Specification window, where you can specify any set of differncing lags.- Moving Average
defines the moving-average part of the model. Select the Set button to open the MA Polynomial Specification window, where you can add any set of moving-average lags grouped into any number of factors.- Estimation Method
specifies the method used to estimate the model parameters. The Conditional Least Squares and Unconditional Least Squares methods generally require fewer computing resources and are more likely to succeed in fitting complex models. The Maximum Likelihood method requires more resources but provides a better fit in some cases. See also Estimation Details in Chapter 7, The ARIMA Procedure.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.