Printing Options

NOPRINT

suppresses all printed output.

Input Data Options

DATA=SAS-data-set

specifies the name of the SAS data set to be used by the procedure. If the DATA= option is omitted, the most recently created SAS data set is used.

LAGMAX=k

specifies the number of lags for which the sample autocovariance matrix is computed. The LAGMAX= option controls the number of lags printed in the schematic representation of the autocorrelations.

The sample autocovariance matrix of lag i, denoted as 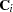, is computed as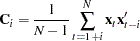

where 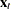is the differenced and centered data and 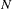is the number of observations. (If the NOCENTER option is specified, 1 is not subtracted from 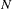.) LAGMAX= k specifies that through are computed. The default is LAGMAX=10.

NOCENTER

prevents subtraction of the sample mean from the input series (after any specified differencing) before the analysis.

Options for Preliminary Autoregressive Models

ARMAX=n

specifies the maximum order of the preliminary autoregressive models. The ARMAX= option controls the autoregressive orders for which information criteria are printed, and controls the number of lags printed in the schematic representation of partial autocorrelations. The default is ARMAX=10. See the section Preliminary Autoregressive Models for details.

MINIC

writes to the OUTAR= data set only the preliminary Yule-Walker estimates for the VAR model that produces the minimum AIC. See the section OUTAR= Data Set for details.

OUTAR=SAS-data-set

writes the Yule-Walker estimates of the preliminary autoregressive models to a SAS data set. See the section OUTAR= Data Set for details.

PRINTOUT=SHORT | LONG | NONE

determines the amount of detail printed. PRINTOUT=LONG prints the lagged covariance matrices, the partial autoregressive matrices, and estimates of the residual covariance matrices from the sequence of autoregressive models. PRINTOUT=NONE suppresses the output for the preliminary autoregressive models. The descriptive statistics and state space model estimation output are still printed when PRINTOUT=NONE is specified. PRINTOUT=SHORT is the default.

Canonical Correlation Analysis Options

CANCORR

prints the canonical correlations and information criterion for each candidate state vector considered. See the section Canonical Correlation Analysis Options for details.

DIMMAX=n

specifies the upper limit to the dimension of the state vector. The DIMMAX= option can be used to limit the size of the model selected. The default is DIMMAX=10.

PASTMIN=n

specifies the minimum number of lags to include in the canonical correlation analysis. The default is PASTMIN=0. See the section Canonical Correlation Analysis Options for details.

SIGCORR=value

specifies the multiplier of the degrees of freedom for the penalty term in the information criterion used to select the state space form. The default is SIGCORR=2. The larger the value of the SIGCORR= option, the smaller the state vector tends to be. Hence, a large value causes a simpler model to be fit. See the section Canonical Correlation Analysis Options for details.

State Space Model Estimation Options

COVB

prints the inverse of the observed information matrix for the parameter estimates. This matrix is an estimate of the covariance matrix for the parameter estimates.

DETTOL=value

specifies the convergence criterion. The DETTOL= and PARMTOL= option values are used together to test for convergence of the estimation process. If, during an iteration, the relative change of the parameter estimates is less than the PARMTOL= value and the relative change of the determinant of the innovation variance matrix is less than the DETTOL= value, then iteration ceases and the current estimates are accepted. The default is DETTOL=1E–5.

ITPRINT

prints the iterations during the estimation process.

KLAG=n

sets an upper limit for the number of lags of the sample autocovariance matrix used in computing the approximate likelihood function. If the data have a strong moving average character, a larger KLAG= value might be necessary to obtain good estimates. The default is KLAG=15. See the section Parameter Estimation for details.

MAXIT=n

sets an upper limit to the number of iterations in the maximum likelihood or conditional least squares estimation. The default is MAXIT=50.

NOEST

suppresses the final maximum likelihood estimation of the selected model.

OUTMODEL=SAS-data-set

writes the parameter estimates and their standard errors to a SAS data set. See the section OUTMODEL= Data Set for details.

PARMTOL=value

specifies the convergence criterion. The DETTOL= and PARMTOL= option values are used together to test for convergence of the estimation process. If, during an iteration, the relative change of the parameter estimates is less than the PARMTOL= value and the relative change of the determinant of the innovation variance matrix is less than the DETTOL= value, then iteration ceases and the current estimates are accepted. The default is PARMTOL=0.001.

RESIDEST

computes the final estimates by using conditional least squares on the raw data. This type of estimation might be more stable than the default maximum likelihood method but is usually more computationally expensive. See the section Parameter Estimation for details about the conditional least squares method.

SINGULAR=value

specifies the criterion for testing for singularity of a matrix. A matrix is declared singular if a scaled pivot is less than the SINGULAR= value when sweeping the matrix. The default is SINGULAR=1E–7.

Forecasting Options

BACK=n

starts forecasting n periods before the end of the input data. The BACK= option value must not be greater than the number of observations. The default is BACK=0.

INTERVAL=interval

specifies the time interval between observations. The INTERVAL= value is used in conjunction with the ID variable to check that the input data are in order and have no missing periods. The INTERVAL= option is also used to extrapolate the ID values past the end of the input data. See Chapter 4, Date Intervals, Formats, and Functions, for details about the INTERVAL= values allowed.

INTPER=n

specifies that each input observation corresponds to n time periods. For example, the options INTERVAL=MONTH and INTPER=2 specify bimonthly data and are equivalent to specifying INTERVAL=MONTH2. If the INTERVAL= option is not specified, the INTPER= option controls the increment used to generate ID values for the forecast observations. The default is INTPER=1.

LEAD=n

specifies how many forecast observations are produced. The forecasts start at the point set by the BACK= option. The default is LEAD=0, which produces no forecasts.

OUT=SAS-data-set

writes the residuals, actual values, forecasts, and forecast standard errors to a SAS data set. See the section OUT= Data Set for details.

PRINT

prints the forecasts.