| The SPECTRA Procedure |
| WEIGHTS Statement |
- WEIGHTS weight-constants | kernel-specification ;
The WEIGHTS statement specifies the relative weights used in the moving average applied to the periodogram ordinates to form the spectral density estimates. A WEIGHTS statement must be used to produce smoothed spectral density estimates. You can specify the relative weights in two ways: you can specify them explicitly as explained in the section Using Weight Constants Specification, or you can specify them implicitly by using the kernel specification as explained in the section Using Kernel Specifications. If the WEIGHTS statement is not used, only the periodogram is produced.
Using Weight Constants Specification
Any number of weighting constants can be specified. The constants should be positive and symmetric about the middle weight. The middle constant (or the constant to the right of the middle if an even number of weight constants are specified) is the relative weight of the current periodogram ordinate. The constant immediately following the middle one is the relative weight of the next periodogram ordinate, and so on. The actual weights used in the smoothing process are the weights specified in the WEIGHTS statement scaled so that they sum to 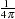 .
.
The moving average reflects at each end of the periodogram. The first periodogram ordinate is not used; the second periodogram ordinate is used in its place.
For example, a simple triangular weighting can be specified using the following WEIGHTS statement:
weights 1 2 3 2 1;
Using Kernel Specifications
You can specify five different kernels in the WEIGHTS statement. The syntax for the statement is
- WEIGHTS [PARZEN][BART][TUKEY][TRUNCAT][QS] [c e] ;
where 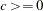 and
and 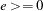 are used to compute the bandwidth parameter as
are used to compute the bandwidth parameter as
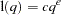 |
and  is the number of periodogram ordinates +1:
is the number of periodogram ordinates +1:
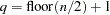 |
To specify the bandwidth explicitly, set 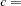 to the desired bandwidth and
to the desired bandwidth and 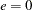 .
.
For example, a Parzen kernel can be specified using the following WEIGHTS statement:
weights parzen 0.5 0;
For details, see the section Kernels.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.