| The QLIM Procedure |
Example 21.2 Tobit Analysis
The following statements show a subset of the Mroz (1987) data set. In these data, Hours is the number of hours the wife worked outside the household in a given year, Yrs_Ed is the years of education, and Yrs_Exp is the years of work experience. A Tobit model will be fit to the hours worked with years of education and experience as covariates.
By the nature of the data it is clear that there are a number of women who committed some positive number of hours to outside work (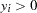 is observed). There are also a number of women who did not work at all (
is observed). There are also a number of women who did not work at all (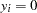 is observed). This gives us the following model:
is observed). This gives us the following model:
 |
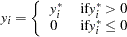 |
where 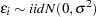 . The set of explanatory variables is denoted by
. The set of explanatory variables is denoted by 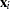 .
.
title1 'Estimating a Tobit model';
data subset;
input Hours Yrs_Ed Yrs_Exp @@;
if Hours eq 0 then Lower=.;
else Lower=Hours;
datalines;
0 8 9 0 8 12 0 9 10 0 10 15 0 11 4 0 11 6
1000 12 1 1960 12 29 0 13 3 2100 13 36
3686 14 11 1920 14 38 0 15 14 1728 16 3
1568 16 19 1316 17 7 0 17 15
;
/*-- Tobit Model --*/
proc qlim data=subset;
model hours = yrs_ed yrs_exp;
endogenous hours ~ censored(lb=0);
run;
The output of the QLIM procedure is shown in Output 21.2.1.
| Model Fit Summary | |
|---|---|
| Number of Endogenous Variables | 1 |
| Endogenous Variable | hours |
| Number of Observations | 17 |
| Log Likelihood | -74.93700 |
| Maximum Absolute Gradient | 1.18953E-6 |
| Number of Iterations | 23 |
| Optimization Method | Quasi-Newton |
| AIC | 157.87400 |
| Schwarz Criterion | 161.20685 |
In the “Parameter Estimates” table there are four rows. The first three of these rows correspond to the vector estimate of the regression coefficients 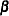 . The last one is called _Sigma, which corresponds to the estimate of the error variance
. The last one is called _Sigma, which corresponds to the estimate of the error variance  .
.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.