| The QLIM Procedure |
| Introductory Example: Binary Probit and Logit Models |
The following example illustrates the use of PROC QLIM. The data were originally published by Mroz (1987) and downloaded from Wooldridge (2002). This data set is based on a sample of 753 married white women. The dependent variable is a discrete variable of labor force participation (inlf ). Explanatory variables are the number of children ages 5 or younger (kidslt6 ), the number of children ages 6 to 18 (kidsge6 ), the woman’s age (age ), the woman’s years of schooling (educ ), wife’s labor experience (exper ), square of experience (expersq ), and the family income excluding the wife’s wage (nwifeinc ). The program (with data values omitted) is as follows:
/*-- Binary Probit --*/
proc qlim data=mroz;
model inlf = nwifeinc educ exper expersq
age kidslt6 kidsge6 / discrete;
run;
Results of this analysis are shown in the following four figures. In the first table, shown in Figure 21.1, PROC QLIM provides frequency information about each choice. In this example, 428 women participate in the labor force (inlf =1).
| Discrete Response Profile of inlf | |||
|---|---|---|---|
| Index | Value | Frequency | Percent |
| 1 | 0 | 325 | 43.16 |
| 2 | 1 | 428 | 56.84 |
The second table is the estimation summary table shown in Figure 21.2. Included are the number of dependent variables, names of dependent variables, the number of observations, the log-likelihood function value, the maximum absolute gradient, the number of iterations, AIC, and Schwarz criterion.
Goodness-of-fit measures are displayed in Figure 21.3. All measures except McKelvey-Zavoina’s definition are based on the log-likelihood function value. The likelihood ratio test statistic has chi-square distribution conditional on the null hypothesis that all slope coefficients are zero. In this example, the likelihood ratio statistic is used to test the hypothesis that kidslt6  kidge6
kidge6  age
age  educ
educ  exper
exper  expersq
expersq  nwifeinc
nwifeinc 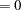 .
.
| Goodness-of-Fit Measures | ||
|---|---|---|
| Measure | Value | Formula |
| Likelihood Ratio (R) | 227.14 | 2 * (LogL - LogL0) |
| Upper Bound of R (U) | 1029.7 | - 2 * LogL0 |
| Aldrich-Nelson | 0.2317 | R / (R+N) |
| Cragg-Uhler 1 | 0.2604 | 1 - exp(-R/N) |
| Cragg-Uhler 2 | 0.3494 | (1-exp(-R/N)) / (1-exp(-U/N)) |
| Estrella | 0.2888 | 1 - (1-R/U)^(U/N) |
| Adjusted Estrella | 0.2693 | 1 - ((LogL-K)/LogL0)^(-2/N*LogL0) |
| McFadden's LRI | 0.2206 | R / U |
| Veall-Zimmermann | 0.4012 | (R * (U+N)) / (U * (R+N)) |
| McKelvey-Zavoina | 0.4025 | |
| N = # of observations, K = # of regressors | ||
Finally, the parameter estimates and standard errors are shown in Figure 21.4.
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | t Value | Approx Pr > |t| |
| Intercept | 1 | 0.270077 | 0.508590 | 0.53 | 0.5954 |
| nwifeinc | 1 | -0.012024 | 0.004840 | -2.48 | 0.0130 |
| educ | 1 | 0.130905 | 0.025255 | 5.18 | <.0001 |
| exper | 1 | 0.123348 | 0.018720 | 6.59 | <.0001 |
| expersq | 1 | -0.001887 | 0.000600 | -3.14 | 0.0017 |
| age | 1 | -0.052853 | 0.008477 | -6.24 | <.0001 |
| kidslt6 | 1 | -0.868329 | 0.118519 | -7.33 | <.0001 |
| kidsge6 | 1 | 0.036005 | 0.043477 | 0.83 | 0.4076 |
When the error term has a logistic distribution, the binary logit model is estimated. To specify a logistic distribution, add D=LOGIT option as follows:
/*-- Binary Logit --*/
proc qlim data=mroz;
model inlf = nwifeinc educ exper expersq
age kidslt6 kidsge6 / discrete(d=logit);
run;
The estimated parameters are shown in Figure 21.5.
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | t Value | Approx Pr > |t| |
| Intercept | 1 | 0.425452 | 0.860365 | 0.49 | 0.6210 |
| nwifeinc | 1 | -0.021345 | 0.008421 | -2.53 | 0.0113 |
| educ | 1 | 0.221170 | 0.043441 | 5.09 | <.0001 |
| exper | 1 | 0.205870 | 0.032070 | 6.42 | <.0001 |
| expersq | 1 | -0.003154 | 0.001017 | -3.10 | 0.0019 |
| age | 1 | -0.088024 | 0.014572 | -6.04 | <.0001 |
| kidslt6 | 1 | -1.443354 | 0.203575 | -7.09 | <.0001 |
| kidsge6 | 1 | 0.060112 | 0.074791 | 0.80 | 0.4215 |
The heteroscedastic logit model can be estimated using the HETERO statement. If the variance of the logit model is a function of the family income level excluding wife’s income (nwifeinc ), the variance can be specified as
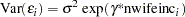 |
where 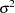 is normalized to 1 because the dependent variable is discrete. The following SAS statements estimate the heteroscedastic logit model:
is normalized to 1 because the dependent variable is discrete. The following SAS statements estimate the heteroscedastic logit model:
/*-- Binary Logit with Heteroscedasticity --*/
proc qlim data=mroz;
model inlf = nwifeinc educ exper expersq
age kidslt6 kidsge6 / discrete(d=logit);
hetero inlf ~ nwifeinc / noconst;
run;
The parameter estimate,  , of the heteroscedasticity variable is listed as _H.nwifeinc; see Figure 21.6.
, of the heteroscedasticity variable is listed as _H.nwifeinc; see Figure 21.6.
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | t Value | Approx Pr > |t| |
| Intercept | 1 | 0.510445 | 0.983538 | 0.52 | 0.6038 |
| nwifeinc | 1 | -0.026778 | 0.012108 | -2.21 | 0.0270 |
| educ | 1 | 0.255547 | 0.061728 | 4.14 | <.0001 |
| exper | 1 | 0.234105 | 0.046639 | 5.02 | <.0001 |
| expersq | 1 | -0.003613 | 0.001236 | -2.92 | 0.0035 |
| age | 1 | -0.100878 | 0.021491 | -4.69 | <.0001 |
| kidslt6 | 1 | -1.645206 | 0.311296 | -5.29 | <.0001 |
| kidsge6 | 1 | 0.066941 | 0.085633 | 0.78 | 0.4344 |
| _H.nwifeinc | 1 | 0.013280 | 0.013606 | 0.98 | 0.3291 |
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.