Example 19.1 Analyzing Demand for Liquid Assets
In this example, the demand equations for liquid assets are estimated. The demand function for the demand deposits is estimated under three error structures while demand equations for time deposits and savings and loan (S&L) association shares are calculated using the Parks method. The data for seven states (CA, DC, FL, IL, NY, TX, and WA) are selected out of 49 states. See Feige (1964) for data description. All variables were transformed via natural logarithm. The data set A is shown below.
data a;
length state $ 2;
input state $ year d t s y rd rt rs;
label d = 'Per Capita Demand Deposits'
t = 'Per Capita Time Deposits'
s = 'Per Capita S & L Association Shares'
y = 'Permanent Per Capita Personal Income'
rd = 'Service Charge on Demand Deposits'
rt = 'Interest on Time Deposits'
rs = 'Interest on S & L Association Shares';
datalines;
CA 1949 6.2785 6.1924 4.4998 7.2056 -1.0700 0.1080 1.0664
CA 1950 6.4019 6.2106 4.6821 7.2889 -1.0106 0.1501 1.0767
CA 1951 6.5058 6.2729 4.8598 7.3827 -1.0024 0.4008 1.1291
CA 1952 6.4785 6.2729 5.0039 7.4000 -0.9970 0.4492 1.1227
CA 1953 6.4118 6.2538 5.1761 7.4200 -0.8916 0.4662 1.2110
... more lines ...
As shown in the following statements, the SORT procedure is used to sort the data into the required time series cross-sectional format; then PROC PANEL analyzes the data.
proc sort data=a;
by state year;
run;
proc panel data=a;
model d = y rd rt rs / fuller parks dasilva m=7;
model t = y rd rt rs / parks;
model s = y rd rt rs / parks;
id state year;
run;
The income elasticities for liquid assets are greater than 1 except for the demand deposit income elasticity (0.692757) estimated by the Da Silva method. In Output 19.1.1, Output 19.1.2, and Output 19.1.3, the coefficient estimates (–0.29094, –0.43591, and –0.27736) of demand deposits (RD) imply that demand deposits increase significantly as the service charge is reduced. The price elasticities (0.227152 and 0.408066) for time deposits (RT) and S&L association shares (RS) have the expected sign. Thus an increase in the interest rate on time deposits or S&L shares will increase the demand for the corresponding liquid asset. Demand deposits and S&L shares appear to be substitutes (see Output 19.1.2, Output 19.1.3, and Output 19.1.5). Time deposits are also substitutes for S&L shares in the time deposit demand equation (see Output 19.1.4), while these liquid assets are independent of each other in Output 19.1.5 (insignificant coefficient estimate of RT, 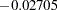 ). Demand deposits and time deposits appear to be weak complements in Output 19.1.3 and Output 19.1.4, while the cross elasticities between demand deposits and time deposits are not significant in Output 19.1.2 and Output 19.1.5.
). Demand deposits and time deposits appear to be weak complements in Output 19.1.3 and Output 19.1.4, while the cross elasticities between demand deposits and time deposits are not significant in Output 19.1.2 and Output 19.1.5.
Output 19.1.1
Demand for Demand Deposits, Fuller-Battese Method
The PANEL Procedure
Fuller and Battese Variance Components (RanTwo)
Dependent Variable: d Per Capita Demand Deposits
| 0.0795 |
72 |
| 0.0011 |
0.0332 |
| 0.6786 |
|
| 1 |
-1.23606 |
0.7252 |
-1.70 |
0.0926 |
Intercept |
| 1 |
1.064058 |
0.1040 |
10.23 |
<.0001 |
Permanent Per Capita Personal Income |
| 1 |
-0.29094 |
0.0526 |
-5.53 |
<.0001 |
Service Charge on Demand Deposits |
| 1 |
0.039388 |
0.0278 |
1.42 |
0.1603 |
Interest on Time Deposits |
| 1 |
-0.32662 |
0.1140 |
-2.86 |
0.0055 |
Interest on S & L Association Shares |
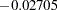 ). Demand deposits and time deposits appear to be weak complements in Output 19.1.3 and Output 19.1.4, while the cross elasticities between demand deposits and time deposits are not significant in Output 19.1.2 and Output 19.1.5.
). Demand deposits and time deposits appear to be weak complements in Output 19.1.3 and Output 19.1.4, while the cross elasticities between demand deposits and time deposits are not significant in Output 19.1.2 and Output 19.1.5.