| The PANEL Procedure |
| Introductory Example |
The following statements use the cost function data from Greene (1990) to estimate the variance components model. The variable PRODUCTION is the log of output in millions of kilowatt-hours, and COST is the log of cost in millions of dollars. Refer to Greene (1990) for details.
data greene;
input firm year production cost @@;
datalines;
1 1955 5.36598 1.14867 1 1960 6.03787 1.45185
1 1965 6.37673 1.52257 1 1970 6.93245 1.76627
2 1955 6.54535 1.35041 2 1960 6.69827 1.71109
2 1965 7.40245 2.09519 2 1970 7.82644 2.39480
... more lines ...
You decide to fit the following model to the data:
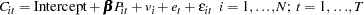 |
where 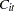 and
and 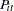 represent the cost and production, and
represent the cost and production, and 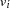 ,
, 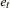 and
and 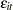 are the cross-sectional, time series, and error variance components.
are the cross-sectional, time series, and error variance components.
If you assume that the time and cross-sectional effects are random, you are left with four possible estimators for the variance components. You choose Fuller-Battese.
The following statements fit this model.
proc sort data=greene;
by firm year;
run;
proc panel data=greene;
model cost = production / rantwo vcomp = fb;
id firm year;
run;
The PANEL procedure output is shown in Figure 19.1. A model description is printed first, which reports the estimation method used and the number of cross sections and time periods. The variance components estimates are printed next. Finally, the table of regression parameter estimates shows the estimates, standard errors, and t tests.
| Model Description | |
|---|---|
| Estimation Method | RanTwo |
| Number of Cross Sections | 6 |
| Time Series Length | 4 |
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.