Example 18.12 Cauchy Distribution Estimation

In this example a nonlinear model is estimated by using the Cauchy distribution. Then a simulation is done for one observation in the data.

The following DATA step creates the data for the model.

   /* Generate a Cauchy distributed Y */
   data c;
      format date monyy.;
      call streaminit(156789);
      do t=0 to 20 by 0.1;
         date=intnx('month','01jun90'd,(t*10)-1);
         x=rand('normal');
         e=rand('cauchy') + 10 ;
         y=exp(4*x)+e;
         output;
      end;
   run;

The model to be estimated is

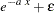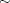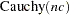That is, the residuals of the model are distributed as a Cauchy distribution with noncentrality parameter .

The log likelihood for the Cauchy distribution is

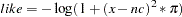The following SAS statements specify the model and the log-likelihood function.

   title1 'Cauchy Distribution';
   
   proc model data=c ;
      dependent y;
      parm a -2 nc 4;
      y=exp(-a*x);
   
          /* Likelihood function for the residuals */
      obj = log(1+(-resid.y-nc)**2 * 3.1415926);
   
      errormodel y ~ general(obj) cdf=cauchy(nc);
   
      fit y / outsn=s1 method=marquardt;
      solve y / sdata=s1 data=c(obs=1) random=1000
                seed=256789 out=out1;
   run;
   
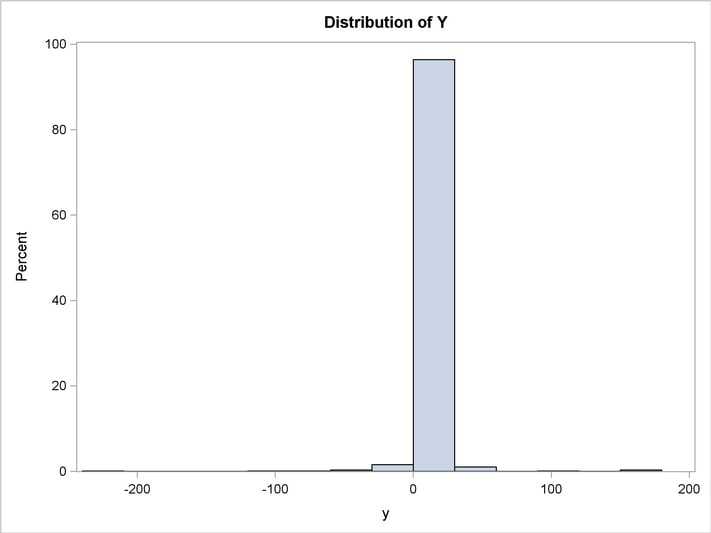
   title 'Distribution of Y';
   proc sgplot data=out1;
      histogram y;
   run;

The FIT statement uses the OUTSN= option to output the 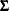matrix for residuals from the normal distribution. The 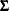matrix is 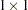and has value 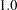because it is a correlation matrix. The OUTS= matrix is the scalar 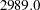. Because the distribution is univariate (no covariances), the OUTS= option would produce the same simulation results. The simulation is performed by using the SOLVE statement.

The distribution of is shown in the following output.

Output 18.12.1 Distribution of Y