Details: ENTROPY Procedure

Shannon’s measure of entropy for a distribution is given by

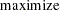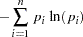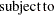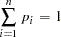where 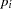is the probability associated with the ith support point. Properties that characterize the entropy measure are set forth by Kapur and Kesavan (1992).

The objective is to maximize the entropy of the distribution with respect to the probabilities 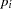and subject to constraints that reflect any other known information about the distribution (Jaynes; 1957). This measure, in the absence of additional information, reaches a maximum when the probabilities are uniform. A distribution other than the uniform distribution arises from information already known.