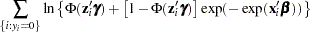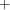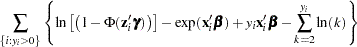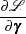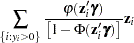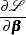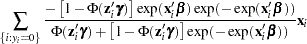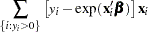In the zero-inflated Poisson (ZIP) regression model, the data generation process referred to earlier as Process 2 is
where 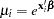 . Thus the ZIP model is defined as
. Thus the ZIP model is defined as
The conditional expectation and conditional variance of 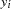 are given by
are given by
Note that the ZIP model (as well as the ZINB model) exhibits overdispersion since 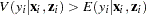 .
.
In general, the log-likelihood function of the ZIP model is
Once a specific link function (either logistic or standard normal) for the probability 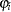 is chosen, it is possible to write the exact expressions for the log-likelihood function and the gradient.
is chosen, it is possible to write the exact expressions for the log-likelihood function and the gradient.
ZIP Model with Logistic Link Function
First, consider the ZIP model in which the probability 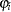 is expressed with a logistic link function, namely
is expressed with a logistic link function, namely
The log-likelihood function is
The gradient for this model is given by
ZIP Model with Standard Normal Link Function
Next, consider the ZIP model in which the probability 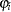 is expressed with a standard normal link function:
is expressed with a standard normal link function: 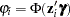 . The log-likelihood function is
. The log-likelihood function is
The gradient for this model is given by
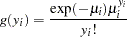
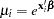 . Thus the ZIP model is defined as
. Thus the ZIP model is defined as 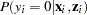


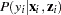

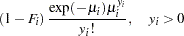
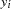 are given by
are given by 
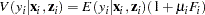
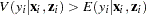 .
. 
 is chosen, it is possible to write the exact expressions for the log-likelihood function and the gradient.
is chosen, it is possible to write the exact expressions for the log-likelihood function and the gradient.  is expressed with a logistic link function, namely
is expressed with a logistic link function, namely 


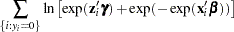


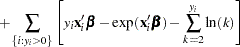


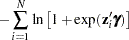
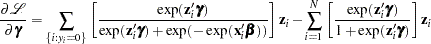

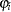 is expressed with a standard normal link function:
is expressed with a standard normal link function: 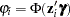 . The log-likelihood function is
. The log-likelihood function is