| The COUNTREG Procedure |
| Negative Binomial Regression |
The Poisson regression model can be generalized by introducing an unobserved heterogeneity term for observation  . Thus, the individuals are assumed to differ randomly in a manner that is not fully accounted for by the observed covariates. This is formulated as
. Thus, the individuals are assumed to differ randomly in a manner that is not fully accounted for by the observed covariates. This is formulated as
 |
where the unobserved heterogeneity term  is independent of the vector of regressors
is independent of the vector of regressors 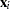 . Then the distribution of
. Then the distribution of 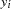 conditional on
conditional on 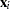 and
and  is Poisson with conditional mean and conditional variance
is Poisson with conditional mean and conditional variance  :
:
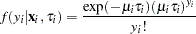 |
Let 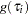 be the probability density function of
be the probability density function of  . Then, the distribution
. Then, the distribution  (no longer conditional on
(no longer conditional on  ) is obtained by integrating
) is obtained by integrating  with respect to
with respect to  :
:
 |
An analytical solution to this integral exists when  is assumed to follow a gamma distribution. This solution is the negative binomial distribution. When the model contains a constant term, it is necessary to assume that
is assumed to follow a gamma distribution. This solution is the negative binomial distribution. When the model contains a constant term, it is necessary to assume that  , in order to identify the mean of the distribution. Thus, it is assumed that
, in order to identify the mean of the distribution. Thus, it is assumed that  follows a gamma(
follows a gamma( ) distribution with
) distribution with  and
and  :
:
 |
where  is the gamma function and
is the gamma function and 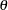 is a positive parameter. Then, the density of
is a positive parameter. Then, the density of  given
given  is derived as
is derived as
 |
 |
 |
|||
 |
 |
 |
|||
 |
 |
 |
|||
 |
 |
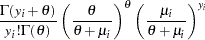 |
Making the substitution  (
(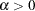 ), the negative binomial distribution can then be rewritten as
), the negative binomial distribution can then be rewritten as
 |
Thus, the negative binomial distribution is derived as a gamma mixture of Poisson random variables. It has conditional mean
 |
and conditional variance
 |
The conditional variance of the negative binomial distribution exceeds the conditional mean. Overdispersion results from neglected unobserved heterogeneity. The negative binomial model with variance function  , which is quadratic in the mean, is referred to as the NEGBIN2 model (Cameron and Trivedi 1986). To estimate this model, specify DIST=NEGBIN(p=2) in the MODEL statement. The Poisson distribution is a special case of the negative binomial distribution where
, which is quadratic in the mean, is referred to as the NEGBIN2 model (Cameron and Trivedi 1986). To estimate this model, specify DIST=NEGBIN(p=2) in the MODEL statement. The Poisson distribution is a special case of the negative binomial distribution where  . A test of the Poisson distribution can be carried out by testing the hypothesis that
. A test of the Poisson distribution can be carried out by testing the hypothesis that  . A Wald test of this hypothesis is provided (it is the reported
. A Wald test of this hypothesis is provided (it is the reported  statistic for the estimated
statistic for the estimated  in the negative binomial model).
in the negative binomial model).
The log-likelihood function of the negative binomial regression model (NEGBIN2) is given by
 |
 |
 |
|||
 |
 |
 |
where use of the following fact is made:
 |
if  is an integer.
is an integer.
The gradient is
 |
and
 |
Cameron and Trivedi (1986) consider a general class of negative binomial models with mean 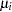 and variance function
and variance function  . The NEGBIN2 model, with
. The NEGBIN2 model, with  , is the standard formulation of the negative binomial model. Models with other values of
, is the standard formulation of the negative binomial model. Models with other values of  ,
,  , have the same density
, have the same density  except that
except that  is replaced everywhere by
is replaced everywhere by  . The negative binomial model NEGBIN1, which sets
. The negative binomial model NEGBIN1, which sets  , has variance function
, has variance function  , which is linear in the mean. To estimate this model, specify DIST=NEGBIN(p=1) in the MODEL statement.
, which is linear in the mean. To estimate this model, specify DIST=NEGBIN(p=1) in the MODEL statement.
The log-likelihood function of the NEGBIN1 regression model is given by
 |
 |
 |
|||
 |
 |
 |
The gradient is
 |
and
 |
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.