| The COUNTREG Procedure |
Getting Started: COUNTREG Procedure
The COUNTREG procedure is similar in use to other regression model procedures in the SAS System. For example, the following statements are used to estimate a Poisson regression model:
proc countreg data=one ;
model y = x / dist=poisson ;
run;
The response variable  is numeric and has nonnegative integer values. To allow for variance greater than the mean, specify the dist=negbin option to fit the negative binomial model instead of the Poisson.
is numeric and has nonnegative integer values. To allow for variance greater than the mean, specify the dist=negbin option to fit the negative binomial model instead of the Poisson.
The following example illustrates the use of PROC COUNTREG. The data are taken from Long (1997). This study examines how factors such as gender (fem), marital status (mar), number of young children (kid5), prestige of the graduate program (phd), and number of articles published by a scientist’s mentor (ment) affect the number of articles (art) published by the scientist.
The first 10 observations are shown in Figure 10.1.
The following SAS statements estimate the Poisson regression model:
/*-- Poisson Regression --*/
proc countreg data=long97data;
model art = fem mar kid5 phd ment / dist=poisson method=quanew;
run;
The Model Fit Summary, shown in Figure 10.2, lists several details about the model. By default, the COUNTREG procedure uses the Newton-Raphson optimization technique. The maximum log-likelihood value is shown, as well as two information measures, Akaike’s information criterion (AIC) and Schwarz’s Bayesian information criterion (SBC), which can be used to compare competing Poisson models. Smaller values of these criteria indicate better models.
| Model Fit Summary | |
|---|---|
| Dependent Variable | art |
| Number of Observations | 915 |
| Data Set | WORK.LONG97DATA |
| Model | Poisson |
| Log Likelihood | -1651 |
| Maximum Absolute Gradient | 0.00181 |
| Number of Iterations | 13 |
| Optimization Method | Quasi-Newton |
| AIC | 3314 |
| SBC | 3343 |
The parameter estimates of the model and their standard errors are shown in Figure 10.3. All covariates are significant predictors of the number of articles, except for the prestige of the program (phd), which has a  -value of 0.6271.
-value of 0.6271.
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | t Value | Approx Pr > |t| |
| Intercept | 1 | 0.304617 | 0.102982 | 2.96 | 0.0031 |
| fem | 1 | -0.224594 | 0.054614 | -4.11 | <.0001 |
| mar | 1 | 0.155243 | 0.061375 | 2.53 | 0.0114 |
| kid5 | 1 | -0.184883 | 0.040127 | -4.61 | <.0001 |
| phd | 1 | 0.012823 | 0.026397 | 0.49 | 0.6271 |
| ment | 1 | 0.025543 | 0.002006 | 12.73 | <.0001 |
The following statements fit the negative binomial model. While the Poisson model requires that the conditional mean and conditional variance be equal, the negative binomial model allows for overdispersion; that is, the conditional variance may exceed the conditional mean.
/*-- Negative Binomial Regression --*/
proc countreg data=long97data;
model art = fem mar kid5 phd ment / dist=negbin(p=2) method=quanew;
run;
The fit summary is shown in Figure 10.4, and parameter estimates are listed in Figure 10.5.
| Model Fit Summary | |
|---|---|
| Dependent Variable | art |
| Number of Observations | 915 |
| Data Set | WORK.LONG97DATA |
| Model | NegBin |
| Log Likelihood | -1561 |
| Maximum Absolute Gradient | 1.75584E-6 |
| Number of Iterations | 16 |
| Optimization Method | Quasi-Newton |
| AIC | 3136 |
| SBC | 3170 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | t Value | Approx Pr > |t| |
| Intercept | 1 | 0.256144 | 0.138560 | 1.85 | 0.0645 |
| fem | 1 | -0.216418 | 0.072672 | -2.98 | 0.0029 |
| mar | 1 | 0.150489 | 0.082106 | 1.83 | 0.0668 |
| kid5 | 1 | -0.176415 | 0.053060 | -3.32 | 0.0009 |
| phd | 1 | 0.015271 | 0.036040 | 0.42 | 0.6718 |
| ment | 1 | 0.029082 | 0.003470 | 8.38 | <.0001 |
| _Alpha | 1 | 0.441620 | 0.052967 | 8.34 | <.0001 |
The parameter estimate for _Alpha of 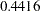 is an estimate of the dispersion parameter in the negative binomial distribution. A
is an estimate of the dispersion parameter in the negative binomial distribution. A  test for the hypothesis
test for the hypothesis  is provided. It is highly significant, indicating overdispersion (
is provided. It is highly significant, indicating overdispersion (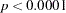 ).
).
The null hypothesis  can be also tested against the alternative
can be also tested against the alternative 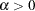 by using the likelihood ratio test, as described by Cameron and Trivedi (1998, pp. 45, 77–78). The likelihood ratio test statistic is equal to
by using the likelihood ratio test, as described by Cameron and Trivedi (1998, pp. 45, 77–78). The likelihood ratio test statistic is equal to 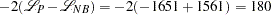 , which is highly significant, providing strong evidence of overdispersion.
, which is highly significant, providing strong evidence of overdispersion.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.