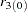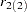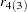The extended sample autocorrelation function (ESACF) method can tentatively identify the orders of a stationary or nonstationary ARMA process based on iterated least squares estimates of the autoregressive parameters. Tsay and Tiao (1984) proposed the technique, and Choi (1992) provides useful descriptions of the algorithm.

Given a stationary or nonstationary time series 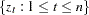with mean corrected form 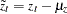with a true autoregressive order of 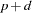and with a true moving-average order of , you can use the ESACF method to estimate the unknown orders 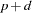and by analyzing the autocorrelation functions associated with filtered series of the form

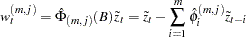where represents the backshift operator, where are the autoregressive test orders, where are the moving-average test orders, and where are the autoregressive parameter estimates under the assumption that the series is an ARMA() process.

For purely autoregressive models (), ordinary least squares (OLS) is used to consistently estimate 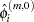. For ARMA models, consistent estimates are obtained by the iterated least squares recursion formula, which is initiated by the pure autoregressive estimates:

The th lag of the sample autocorrelation function of the filtered series is the extended sample autocorrelation function, and it is denoted as .

The standard errors of are computed in the usual way by using Bartlett’s approximation of the variance of the sample autocorrelation function, .

If the true model is an ARMA () process, the filtered series follows an MA() model for so that

Additionally, Tsay and Tiao (1984) show that the extended sample autocorrelation satisfies

where 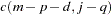is a nonzero constant or a continuous random variable bounded by –1 and 1.

An ESACF table is then constructed by using the for and to identify the ARMA orders (see Table 7.4). The orders are tentatively identified by finding a right (maximal) triangular pattern with vertices located at and and in which all elements are insignificant (based on asymptotic normality of the autocorrelation function). The vertex identifies the order. Table 7.5 depicts the theoretical pattern associated with an ARMA(1,2) series.