The HPCOPULA Procedure
There are three basic types of dependence measures: linear correlation, rank correlation, and tail dependence. Linear correlation is given by
The linear correlation coefficient contains very limited information about the joint properties of the variables. A well-known property is that zero correlation does not imply independence, whereas independence implies zero correlation. In addition, there are distinct bivariate distributions that have the same marginal distribution and the same correlation coefficient. These results suggest that caution must be used in interpreting the linear correlation.
Another statistical measure of dependence is rank correlation, which is nonparametric. For example, Kendall’s tau is the covariance
between the sign statistics ![]() and
and ![]() , where
, where ![]() is an independent copy of
is an independent copy of ![]() :
:
The sign function (sometimes written as sgn) is defined as
![\[ \textrm{sign}(x)= \begin{cases} -1 & \mr{if } x \le 0 \\ 0 & \mr{if } x = 0 \\ 1 & \mr{if } x \ge 0 \end{cases} \]](images/etshpug_hpcopula0020.png)
Spearman’s rho is the correlation between the transformed random variables:
The variables are transformed by their distribution functions so that the transformed variables are uniformly distributed
on ![]() . The rank correlations depend only on the copula of the random variables and are indifferent to the marginal distributions.
Like linear correlation, rank correlation has its limitations. In particular, different copulas result in the same rank correlation.
. The rank correlations depend only on the copula of the random variables and are indifferent to the marginal distributions.
Like linear correlation, rank correlation has its limitations. In particular, different copulas result in the same rank correlation.
A third measure, tail dependence, focuses on only part of the joint properties between the variables. Tail dependence measures the dependence when both variables have extreme values. Formally, they can be defined as the conditional probabilities of quantile exceedances. There are two types of tail dependence:
-
Upper tail dependence is defined as
![\[ \lambda _ u(X_1,X_2) \equiv \lim _{q->1^-} P(X_2> F_2^{-1}(q)|X_1>F_1^{-1}(q)) \]](images/etshpug_hpcopula0023.png)
when the limit exists and
![$\lambda _ u \in [0,1]$](images/etshpug_hpcopula0024.png) . Here
. Here 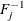 is the quantile function (that is, the inverse of the CDF).
is the quantile function (that is, the inverse of the CDF).
-
Lower tail dependence is defined symmetrically.
