Detecting Rare Cases :: SAS(R) Enterprise Miner(TM) 12.1 Extension Nodes: Developer’s Guide

In data mining, predictive models are often used to detect rare classes. For example, an application to detect credit card fraud might involve a data set containing 100,000 credit card transactions, of which only 100 are fraudulent. Or an analysis of a direct marketing campaign might use a data set representing mailings to 100,000 customers, of whom only 5,000 made a purchase. Since such data are noisy, it is quite possible that no credit card transaction will have a posterior probability over 0.5 of being fraudulent, and that no customer will have a posterior probability over 0.5 of responding. Hence, simply classifying cases according to posterior probability will yield no transactions classified as fraudulent and no customers classified as likely to respond.

When you are collecting the original data, it is always good to over-sample rare classes if possible. If the sample size is fixed, a balanced sample (that is, a nonproportional stratified sample with equal sizes for each class) will usually produce more accurate predictions than an unbalanced 5% / 95% split. For example, if you can sample any 100,000 customers,, it would be much better to have 50,000 responders and 50,000 nonresponders than to have 5,000 responders and 95,000 nonresponders.

Sampling designs like this that are stratified on the classes are called case-control studies or choice-based sampling and have been extensively studied in the statistics and econometrics literature. If a logistic regression model is well-specified for the population ignoring stratification, estimates of the slope parameters from a sample stratified on the classes are unbiased. Estimates of the intercepts are biased but can be easily adjusted to be unbiased, and this adjustment is mathematically equivalent to adjusting the posterior probabilities for prior probabilities.

If you are familiar with survey-sampling methods, you might be tempted to apply sampling weights to analyze a balanced stratified sample. Resist the temptation! In sample surveys, sampling weights (inversely proportional to sampling probability) are used to obtain unbiased estimates of population totals. In predictive modeling, you are not primarily interested in estimating the total number of customers who responded to a mailing, but in identifying which individuals are more likely to respond. Use of sampling weights in a predictive model reduces the effective sample size and makes predictions less accurate. Instead of using sampling weights, specify the appropriate prior probabilities and decision consequences, which will provide all the necessary adjustments for nonproportional stratification on classes.

Unfortunately, balanced sampling is often impractical. The remainder of this section will be concerned with samples where the class sizes are severely unbalanced.

Methods for dealing with the problem of rare classes include:

Specifying correct decision consequences. This is the method of choice with SAS Enterprise Miner, although in some circumstances discussed below, additional methods might also be needed.
Using false prior probabilities. This method is commonly used with software that does not support decision matrices. When there are only two classes, the same decision results can be obtained either by using false priors or by using correct decision matrices. But with three or more classes, false priors do not provide the full power of decision matrices. You should not use false priors with SAS Enterprise Miner, because SAS Enterprise Miner adjusts profit and loss summary statistics for priors. Hence, using false priors might give you false profit and loss summary statistics.
Over-weighting, or weighting rare classes more heavily than common classes during training. This method can be useful when there are three or more classes, but it reduces the effective sample size and can degrade predictive accuracy. Over-weighting can be done in SAS Enterprise Miner by using a frequency variable. However, the current version of SAS Enterprise Miner does not provide full support for sampling weights or other types of weighted analyses, so this method should be approached with care in any analysis where standard errors or significance tests are used, such as stepwise regression. When using a frequency variable for weighting in SAS Enterprise Miner, it is recommended that you also specify appropriate prior probabilities and decision consequences.
Under-sampling, or omitting cases from common classes in the training set. This method throws away information but can be useful for very large data sets in which the amount of information lost is small compared to the noise level in the data. As with over-weighting, the main benefits occur when there are three or more classes. When using under-sampling, it is recommended that you also specify appropriate prior probabilities and decision consequences. Unless you are using this method simply to reduce computational demands, you should not weight cases (using a frequency variable) in inverse proportion to the sampling probabilities, since the use of sampling weights would cancel out the effect of using nonproportional sampling, accomplishing nothing.
Duplicating cases from rare classes in the training set. This method is equivalent to using a frequency variable, except that duplicating cases requires more computer time and disk space. Hence, this method is not recommended except for incremental backprop training in the Neural Network node.

A typical scenario for analyzing data with a rare class would proceed as follows:

In the Input Data node, open a data set containing a random sample of the population. Specify the prior probabilities in the target profile: For a simple random sample, the priors are proportional to the data. For a stratified random sample, you have to enter numbers for the priors. Also specify the decision matrix in the target profile, including a do-nothing decision if applicable. The profit for choosing the best decision for a case from a rare class should be larger than the profit for choosing the best decision for a case from a common class.
You have the option to do the following: For over-weighting, assign a role of Frequency to the weighting variable in the Data Source wizard or Metadata node, or compute a weighting variable in the Transform Variables node. For under-sampling, use the Sampling node to do stratified sampling on the class variable with the Equal Size option.
Use the Data Partition node to create training, validation, and test sets.
Use one or more modeling nodes.
In the Model Comparison node, compare models based on the total or average profit or loss in the validation set.
To produce a profit chart in the Model Comparison node, open the target profile for the model of interest and delete the do-nothing decision.

Specifying correct prior probabilities and decision consequences is generally sufficient to obtain correct decision results if the model that you use is well-specified. A model is well-specified if there exist values for the weights or other parameters in the model that provide a true description of the population, including the distribution of the target noise. However, it is the nature of data mining that you often do not know the true form of the mechanism underlying the data. So in practice it is often necessary to use misspecified models. It is often assumed that trees and neural nets are only asymptotically well-specified.

Over-weighting or under-sampling can improve predictive accuracy when there are three or more classes, including at least one rare class and two or more common classes. If the model is misspecified and lacks sufficient complexity to discriminate all of the classes, the estimation process will emphasize the common classes and neglect the rare classes unless either over-weighting or under-sampling is used. 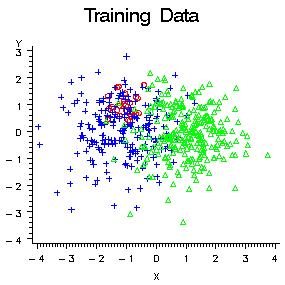For example, consider the data with three classes in the following plot:

The two common classes, blue and green, are separated along the X variable. The rare class, red, is separated from the blue class only along the Y variable. A variable selection method based on significance tests, such as stepwise discriminant analysis, would choose X first, since both the R2 and F statistics would be larger for X. But if you were more interested in detecting the rare class, red, than in distinguishing between the common classes, blue and green, you would prefer to choose Y first.

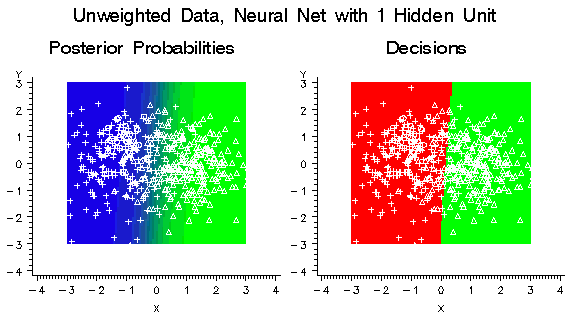
Similarly, if these data were used to train a neural network with one hidden unit, the hidden unit would have a large weight along the X variable. But it would essentially ignore the Y variable, as shown by the posterior probability plot in the following figure. Note that no cases would be classified into the red class using the posterior probabilities for classification. But when a diagonal decision matrix is used, specifying 20 times as much profit for correctly assigning a red case as for correctly assigning a blue or green case, about half the cases are assigned to red, and no cases at all are assigned to blue.

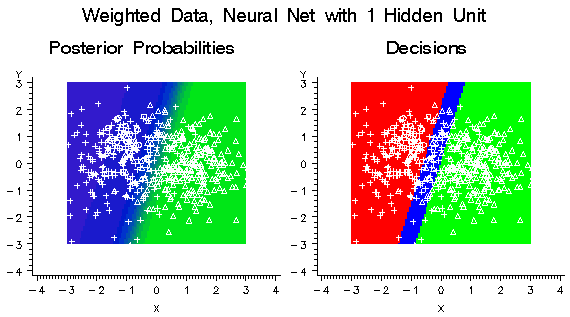
If you weighted the classes in a balanced manner by creating a frequency variable with values inversely proportional to the number of training cases in each class, the hidden unit would learn a linear combination of the X and Y variables. This combination provides moderate discrimination among all three classes instead of high discrimination between the two common classes. But since the model is misspecified, the posterior probabilities are still not accurate. As the following figure shows, there is enough improvement that each class is assigned some cases.

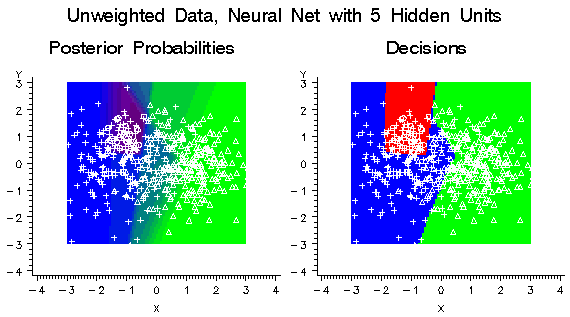
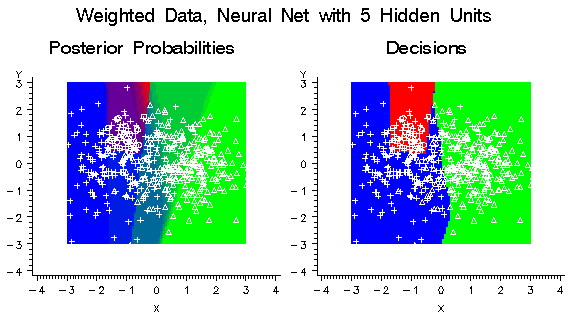
If the neural network had five hidden units instead of just one, it could learn the distributions of all three classes more accurately without the need for weighting, as shown in the following figure:

Using balanced weights for the classes would have only a small effect on the decisions, as shown in the following figure:

Using balanced weights for a well-specified neural network will not usually improve predictive accuracy. But it might make neural network training faster by improving numerical condition and reducing the risk of bad local optima.

Balanced weighting can be important when there are three or more classes. But there is little evidence that balance is important when there are only two classes. Scott and Wild (1989) have shown that for a well-specified logistic regression model, balanced weighting increases the standard error of every linear combination of the regression coefficients and therefore reduces the accuracy of the posterior probability estimates. Simulation studies, which will be described in a separate report, have found that even for misspecified models, balanced weighting provides little improvement and often degrades the total profit or loss in logistic regression, normal-theory discriminant analysis, and neural networks.