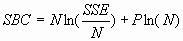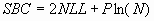Generalization
The critical issue in
predictive modeling is generalization: how well will the model make
predictions for cases that are not in the training set? Data mining
models, like other flexible nonlinear estimation methods such as kernel
regression, can suffer from either underfitting or overfitting (or
as statisticians usually say, oversmoothing or undersmoothing). A
model that is not sufficiently complex can fail to detect fully the
signal in a complicated data set, leading to underfitting. A model
that is too complex might fit the noise, not just the signal, leading
to overfitting. Overfitting can happen even with noise-free data and,
especially in neural nets, can yield predictions that are far beyond
the range of the target values in the training data.
By making a model sufficiently
complex, you can always fit the training data perfectly. For example,
if you have N training cases and you fit a linear regression with
N-1 inputs, you can always get zero error (assuming that the inputs
are not singular). Even if the N-1 inputs are random numbers that
are totally unrelated to the target variable, you will still get zero
error on the training set. However, the predictions are worthless
for such a regression model for new cases that are not in the training
set.
Even if you use only
one continuous input variable, by including enough polynomial terms
in a regression, you can get zero training error. Similarly, you can
always get a perfect fit with only one input variable by growing a
tree large enough or by adding enough hidden units to a neural net.
On the other hand, if
you omit an important input variable from a model, both the training
error and the generalization error will be poor. If you use too few
terms in a regression, or too few hidden units in a neural net, or
too small a tree, then again the training error and the generalization
error might be poor.
Hence, with all types
of data mining models, you must strike a balance between a model that
is too simple and one that is too complex. It is usually necessary
to try a variety of models and then choose a model that is likely
to generalize well.
There are many ways
to choose a model. Some popular methods are heuristic, such as stepwise
regression or CHAID tree modeling, where the model is modified in
a sequence of steps that terminates when no further steps satisfy
a statistical significance criterion. Such heuristic methods might
be of use for developing explanatory models, but they do not directly
address the question of which model will generalize best. The obvious
way to approach this question directly is to estimate the generalization
error of each model, and then choose the model with the smallest estimated
generalization error.
There are many ways
to estimate generalization error, but it is especially important not
to use the training error as an estimate of generalization error.
As previously mentioned, the training error can be very low even when
the generalization error is very high. Choosing a model based on training
error will cause the most complex model to be chosen even if it generalizes
poorly.
A better way to estimate
generalization error is to adjust the training error for the complexity
of the model. In linear least squares regression, this adjustment
is fairly simple if the input variables are assumed fixed or multivariate
normal. Let
Then the average squared
error for the training set is SSE/N, which is designated as ASE by
SAS Enterprise Miner modeling nodes. Statistical software often reports
the mean squared error, MSE=SSE/(N-P).
MSE adjusts the training
error for the complexity of the model by subtracting P in the denominator,
which makes MSE larger than ASE. But MSE is not a good estimate of
the generalization error of the trained model. Under the usual statistical
assumptions, MSE is an unbiased estimate of the generalization error
of the model with the best possible ("true") weights, not
the weights that were obtained by training.
Hence, a stronger adjustment
is required to estimate generalization error of the trained model.
One way to provide a stronger adjustment is to use Akaike's Final
Prediction Error (FPE):
The formula for FPE
multiplies MSE by (N+P)/N, so FPE is larger than MSE. If the input
variables are fixed rather than random, FPE is an unbiased estimate
of the generalization error of the trained model. If inputs and target
are multivariate normal, a further adjustment is required:
The formulas for MSE
and FPE were derived for linear least squares regression. For nonlinear
models and for other training criteria, MSE and FPE are not unbiased.
MSE and FPE might provide adequate approximations if the model is
not too nonlinear and the number of training cases is much larger
than the number of estimated weights. But simulation studies have
shown, especially for neural networks, that FPE is not a good criterion
for model choice, since it does not provide a sufficiently severe
penalty for overfitting.
There are other methods
for adjusting the training error for the complexity of the model.
Two of the most popular criteria for model choice are Schwarz's
Bayesian criterion, (SBC), also called the Bayesian information criterion,
(BIC), and Rissanen's minimum description length principle (MDL).
Although these two criteria were derived from different theoretical
frameworks — SBC from Bayesian statistics and MDL from information
theory — they are essentially the same. In SAS Enterprise Miner,
only the acronym SBC is used. For least squares training,
where NLL is the negative
log likelihood. Smaller values of SBC are better, since smaller values
of SSE or NLL are better. SBC often takes negative values. SBC is
valid for nonlinear models under the usual statistical regularity
conditions. Simulation studies have found that SBC works much better
than FPE for model choice in neural networks.
However, the usual statistical
regularity conditions might not hold for neural networks, so SBC might
not be entirely satisfactory. In tree-based models, there is no well-defined
number of weights, P, in the model, so SBC is not directly applicable.
And other types of models and training methods exist for which no
single-sample statistics such as SBC are known to be good criteria
for model choice. Furthermore, none of these adjustments for model
complexity can be applied to decision processing to maximize total
profit. Fortunately, there are other methods for estimating generalization
error and total profit that are very broadly applicable; these methods
include split-sample or holdout validation, cross validation, and
bootstrapping.
Split-sample validation
is applicable with any type of model and any training method. You
split the available data into a training set and a validation set,
usually by simple random sampling or stratified random sampling. You
train the model using only the training set. You estimate the generalization
error for each model that you train by scoring the validation set.
Then you select the model with the smallest validation error. Split-sample
validation is fast and is often the method of choice for large data
sets. For small data sets, split-sample validation is not so useful
because it does not make efficient use of the data.
For small data sets,
cross validation is generally preferred to split-sample validation.
Cross validation works by splitting the data several ways, training
a different model for each split, and then combining the validation
results across all the splits. In k-fold cross validation, you divide
the data into k subsets of (approximately) equal size. You train the
model k times, each time leaving out one of the subsets from training,
but using only the omitted subset to compute the error criterion.
If k equals the sample size, this is called "leave-one-out"
cross validation.
"Leave-v-out"
is a more elaborate and expensive version of cross validation that
involves leaving out all possible subsets of v cases. Cross validation
makes efficient use of the data because every case is used for both
training and validation. But, of course, cross validation requires
more computer time than split-sample validation. SAS Enterprise Miner
provides leave-one-out cross validation in the Regression node; k-fold
cross validation can be done easily with SAS macros.
In the literature of
artificial intelligence and machine learning, the term "cross
validation" is often applied incorrectly to split-sample validation,
causing much confusion. The distinction between cross validation and
split-sample validation is extremely important because cross validation
can be markedly superior for small data sets. On the other hand, leave-one-out
cross validation might perform poorly for discontinuous error functions
such as the number of misclassified cases, or for discontinuous modeling
methods such as stepwise regression or tree-based models. In such
discontinuous situations, split-sample validation or k-fold cross
validation (usually with k equal to five or ten) are preferred, depending
on the size of the data set.
Bootstrapping seems
to work better than cross validation in many situations, such as stepwise
regression, at the cost of even more computation. In the simplest
form of bootstrapping, instead of repeatedly analyzing subsets of
the data, you repeatedly analyze subsamples of the data. Each subsample
is a random sample with replacement from the full sample. Depending
on what you want to do, anywhere from 200 to 2000 subsamples might
be used. There are many more sophisticated bootstrap methods that
can be used not only for estimating generalization error but also
for estimating bias, standard errors, and confidence bounds.
Not all bootstrapping
methods use resampling from the data — you can also resample
from a nonparametric density estimate, or resample from a parametric
density estimate, or, in some situations, you can use analytical results.
However, bootstrapping does not work well for some methods such as
tree-based models, where bootstrap generalization estimates can be
excessively optimistic.
There has been relatively
little research on bootstrapping neural networks. SAS macros for bootstrap
inference can be obtained from Technical Support.
When numerous models
are compared according to their estimated generalization error (for
example, the error on a validation set), and the model with the lowest
estimated generalization error is chosen for operational use, the
estimate of the generalization error of the selected model will be
optimistic. This optimism is a consequence of the statistical principle
of regression to the mean. Each estimate of generalization error is
subject to random fluctuations. Some models by chance will have an
excessively high estimate of generalization error, but others will
have an excessively low estimate of generalization error.
The model that wins
the competition for lowest generalization error is more likely to
be among the models that by chance have an excessively low estimate
of generalization error. Even if the method for estimating the generalization
error of each model individually provides an unbiased estimate, the
estimate for the winning model will be biased downward. Hence, if
you want an unbiased estimate of the generalization error of the winning
model, further computations are required to obtain such an estimate.
For large data sets,
the most practical way to obtain an unbiased estimate of the generalization
error of the winning model is to divide the data set into three parts,
not just two: the training set, the validation set, and the test set.
The training set is used to train each model. The validation set is
used to choose one of the models. The test data set is used to obtain
an unbiased estimate of the generalization error of the chosen model.
"Since our goal
is to find the network having the best performance on new data, the
simplest approach to the comparison of different networks is to evaluate
the error function using data that is independent of that used for
training. Various networks are trained by minimization of an appropriate
error function defined with respect to a training data set. The performance
of the networks is then compared by evaluating the error function
using an independent validation set, and the network having the smallest
error with respect to the validation set is selected. This approach
is called the hold out method. Since this procedure can itself lead
to some overfitting to the validation set, the performance of the
selected network should be confirmed by measuring its performance
on a third independent set of data called a test set."
Copyright © SAS Institute Inc. All rights reserved.
![Akaike’s FPE = [(SSE(N+P))/(N(N-P))]](images/prede135.png)
![[(SSE(N+1)(N-2))/(N(N-P)(N-P-1))]](images/prede137.png)