Prior Probabilities

For a categorical target variable, each modeling node can estimate posterior probabilities for each class, which are defined as the conditional probabilities of the classes given the input variables. By default, the posterior probabilities are based on implicit prior probabilities that are proportional to the frequencies of the classes in the training set. You can specify different prior probabilities via the Target Profile using the Prior Probabilities tab (see the Target Profile chapter). Also, given a previously scored data set containing posterior probabilities, you can compute new posterior probabilities for different priors by using the DECIDE procedure, which reads the prior probabilities from a decision data set.

Prior probabilities should be specified when the sample proportions of the classes in the training set differ substantially from the proportions in the operational data to be scored, either through sampling variation or deliberate bias. For example, when the purpose of the analysis is to detect a rare class, it is a common practice to use a training set in which the rare class is over represented. If no prior probabilities are used, the estimated posterior probabilities for the rare class will be too high. If you specify correct priors, the posterior probabilities will be correctly adjusted no matter what the proportions in the training set are. For more information, see Detecting Rare Classes.

Increasing the prior probability of a class increases the posterior probability of the class, moving the classification boundary for that class so that more cases are classified into the class. Changing the prior will have a more noticeable effect if the original posterior is near 0.5 than if it is near zero or one.

For linear logistic regression and linear normal-theory discriminant analysis, classification boundaries are hyperplanes; increasing the prior for a class moves the hyperplanes for that class farther from the class mean, while decreasing the prior moves the hyperplanes closer to the class mean. But changing the priors does not change the angles of the hyperplanes.

For quadratic logistic regression and quadratic normal-theory discriminant analysis, classification boundaries are quadratic hypersurfaces; increasing the prior for a class moves the boundaries for that class farther from the class mean, while decreasing the prior moves the boundaries closer to the class mean. But changing the priors does not change the shapes of the quadratic surfaces.

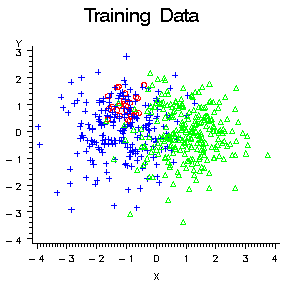
To show the effect of changing prior probabilities, the data in the following figure were generated to have three classes, shown as red circles, blue crosses, and green triangles. Each class has 100 training cases with a bivariate normal distribution.

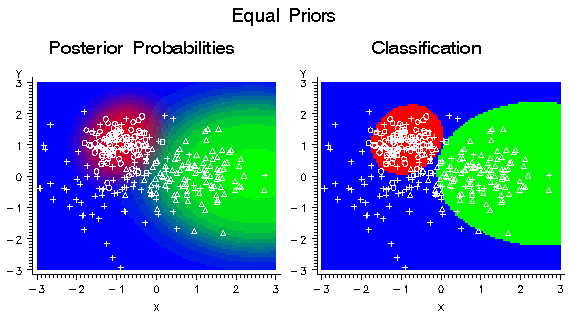
These training data were used to fit a quadratic logistic regression model using the Neural Network engine. Since each class has the same number of training cases, the implicit prior probabilities are equal. In the following figure, the plot on the left shows color-coded posterior probabilities for each class. Bright red areas have a posterior probability near 1.0 for the red circle class, bright blue areas have a posterior probability near 1.0 for the blue cross class, and bright green areas have a posterior probability near 1.0 for the green triangle class. The plot on the right shows the classification results as red, blue, and green regions.

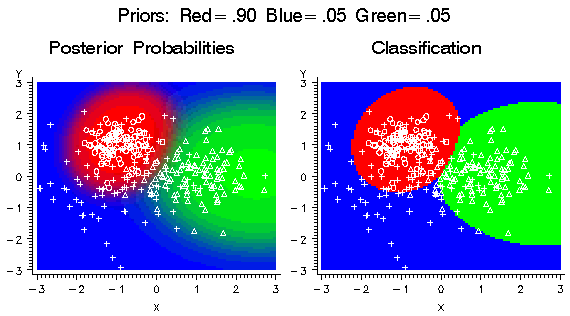
If the prior probability for the red class is increased, the red areas in the plots expand in size as shown in the following figure. The red class has a small variance, so the effect is not widespread. Since the priors for the blue and green classes are still equal, the boundary between blue and green has not changed.

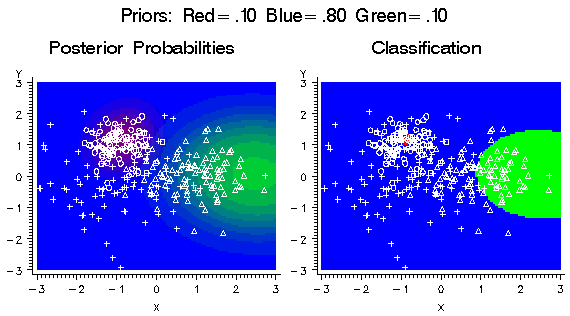
If the prior probability for the blue class is increased, the blue areas in the plots expand in size as shown in the following figure. The blue class has a large variance and has a substantial density extending beyond the high-density red region, so increasing the blue prior causes the red areas to contract dramatically.

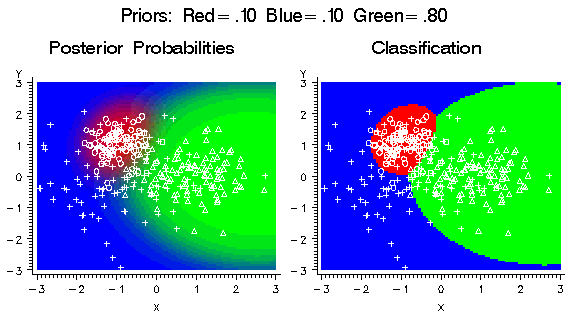
If the prior probability for the green class is increased, the green areas in the plots expand as shown in the following figure.

In the literature on data mining, statistics, pattern recognition, and so on, prior probabilities are used for a variety of purposes that are sometimes confusing. In Enterprise Miner, however, the nodes are designed to use prior probabilities in a simple, unambiguous way:

If you do not explicitly specify prior probabilities (or if you specify None for prior probabilities in the target profile), no adjustments for priors are performed by any nodes.

Posterior probabilities are adjusted for priors as follows. Let:

Then:

For classification, each case i is assigned to the class with the greatest posterior probability, that is, the class t for which Post(i,t) is maximized.

Prior probabilities have no effect on estimating parameters in the Regression node, on learning weights in the Neural Network node, or, by default, on growing trees in the Tree node. Prior probabilities do affect classification and decision processing for each case. Hence, if you specify the appropriate options for each node, prior probabilities can affect the choice of models in the Regression node, early stopping in the Neural Network node, and pruning in the Tree node.

Prior probabilities are also used to adjust the relative contribution of each class when computing the total and average profit and loss as described in the section below on Decisions. The adjustment of total and average profit and loss is distinct from the adjustment of posterior probabilities. The latter is used to obtain correct posteriors for individual cases, whereas the former is used to obtain correct summary statistics for the sample. The adjustment of total and average profit and loss is done only if you explicitly specify prior probabilities; the adjustment is not done when the implicit priors based on the training set proportions are used.

Note that the fit statistics such as misclassification rate and mean squared error are not adjusted for prior probabilities. These fit statistics are intended to provide information about the training process under the assumption that you have provided an appropriate training set with appropriate frequencies. Hence, adjustment for prior probabilities could present a misleading picture of the training results. The profit and loss summary statistics are intended to be used for model selection, and to assess decisions that are made using the model under the assumption that you have provided the appropriate prior probabilities and decision values. Therefore, adjustment for prior probabilities is required for data sets that lack representative class proportions. For more details, see Decisions.

If you specify priors explicitly, Enterprise Miner assumes that the priors that you specify represent the true operational prior probabilities and adjusts the profit and loss summary statistics accordingly. Therefore:

If you do not specify priors, Enterprise Miner assumes that the validation and test sets are representative of the operational data. Hence, the profit and loss summary statistics are not adjusted for the implicit priors based on the training set proportions. Therefore:

If a class has both an old prior and a new prior of zero, then it is omitted from the computations. If a class has a zero old prior, you might not assign it a positive new prior, since that would cause a division by zero. Prior probabilities might not be missing or negative. They must sum to a positive value. If the priors do not sum to one, they are automatically adjusted to do so by dividing each prior by the sum of the priors. A class might have a zero prior probability, but if you use PROC DECIDE to update posterior probabilities, any case having a nonzero posterior corresponding to a zero prior will cause the results for that case to be set to missing values.

To summarize, prior probabilities do not affect:

Prior probabilities do affect:

Prior probabilities will by default affect the following processes if and only if there are two or more decisions in the decision matrix: