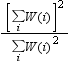Common Features of Predictive Modeling Nodes

The predictive modeling nodes are designed to share many common features. The following table lists some features that are broadly applicable to predictive modeling and indicates which nodes have the features. Decision options, output data sets, and score variables are described in subsequent sections of this chapter.

# — The Regression node treats ordinal inputs as nominal; it does not preserve the ordering of the levels.

Categories for nominal and ordinal variables are defined by the normalized, formatted values of the variable. If you have not explicitly assigned a format to a variable, the default format for a numeric variable is BEST12., and the default format for a character variable is $w., where w is the length of the variable.

Hence, if two values of a variable differ only in the number of leading blanks and in the case of their letters, they will be assigned to the same category. Also, if two values differ only past the first 32 characters (after left justification), they will be assigned to the same category.

Dummy variables are generated for categorical variables in the Regression and Neural Network nodes. If a categorical variable has c categories, the number of dummy variables will be either c or c-1, depending on the role of the variable and what options are specified. The computer time and memory requirements for analyzing a categorical variable with c categories are the same as the requirements for analyzing c or c-1 interval-level variables for the Regression and Neural Network nodes.

When a categorical variable appears in two or more data sets used in the same modeling node, such as the training set (prior to DMDB processing), validation set, and decision data set, the variable is not required to have the same type and length in each data set. For example, a variable named TEMPERAT could be numeric in the training set with values such as 98.6, while a variable by the same name in the validation set could be character with values such as "98.6". As long as the normalized, formatted values from the two data sets agree, the values of the two variables will be matched correctly. In the Neural Network node only, a categorical variable that appears in two or more data sets must have the same formatted length in each data set.

For an interval target variable, by default the modeling nodes try to predict the conditional mean of the target given the values of the input variables. The Neural Network node also provides robust error functions that can be used to predict approximately the conditional median or mode of the target.

For a categorical target variable, by default the modeling nodes try to estimate the conditional probability of each class given the values of the input variables. These conditional probabilities are called posterior probabilities. Given the posterior probabilities, each case can be classified into the most probable class.

You can also specify a profit or loss matrix to classify cases according to the business consequences of the decision. (See the section below on Decisions.) The robust error functions in the Neural Network node can be used to output the approximately most probable class.

When comparing predictive models, it is essential to compare all models using the same cases. If a case is omitted from scoring for one model but not from another (for example, because of missing input variables) you get invalid, "apples-and-oranges" model comparisons. Therefore, Enterprise Miner modeling nodes compute predictions for all cases, even for cases where the model is inapplicable because of missing inputs or other reasons (except, of course, when there are no valid target values).

For cases where the model cannot be applied, the modeling nodes output the unconditional mean (the mean for all cases used for training) for interval targets, or the prior probabilities for categorical targets (see the section below on Prior Probabilities). If you do not specify prior probabilities, implicit priors are used, which are the proportions of the classes among all cases used for training. A variable named _WARN_ in the scored data set indicates why the model could not be applied. If you have lots of cases with missing inputs, you should either use the Decision Tree node for modeling, or use the Impute node to impute missing values before using the Regression or Neural Network nodes.

All of the Enterprise Miner modeling nodes enable you to specify a frequency variable. Typically, the values of the frequency variable are nonnegative integers. The data are treated as if each case were replicated as many times as the value of the frequency variable.

Unlike most SAS procedures, the modeling nodes in Enterprise Miner accept values for a frequency variable that are not integers without truncating the fractional part. Thus, you can use a frequency variable to perform weighted analyses.

However, Enterprise Miner does not provide explicit support for sampling weights, noise-variance weights, or other analyses where the weight variable does not represent the frequency of occurrence of each case. If the frequency variable represents sampling weights or noise-variance weights, the point estimates of regression coefficients and neural network weights will be valid. But if the frequency variable does not represent actual frequencies, then standard errors, significance tests, and statistics such as MSE, AIC, and SBC might be invalid.

If you want to do weighted estimation under the usual assumption for weighted least squares that the weights are inversely proportional to the noise variance (error variance) of the target variable, then you can obtain statistically correct results by specifying frequency values that add up to the sample size.

If you want to use sampling weights that are inversely proportional to the sampling probability of each case, you can get approximate estimates for MSE and related statistics in the Regression and Neural Network nodes by specifying frequencies that add up to the effective sample size. A pessimistic approximation to the effective sample size is provided by

where W(i) is a sampling weight for case i. This approximation will not work properly with the Decision Tree node.