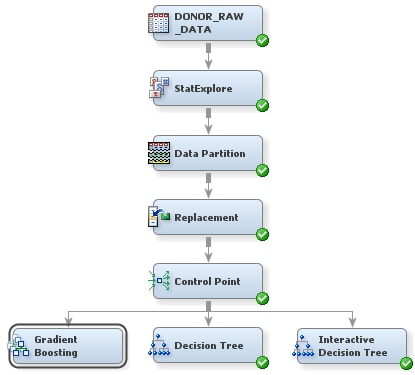
Create a Gradient Boosting Model of the Data

The Gradient Boosting node uses a partitioning algorithm to search for an optimal partition of the data for a single target variable. Gradient boosting is an approach that resamples the analysis data several times to generate results that form a weighted average of the resampled data set. Tree boosting creates a series of decision trees that form a single predictive model.

Like decision trees, boosting makes no assumptions about the distribution of the data. Boosting is less prone to overfit the data than a single decision tree. If a decision tree fits the data fairly well, then boosting often improves the fit. For more information about the Gradient Boosting node, see the SAS Enterprise Miner help documentation.

To create a gradient boosting model of the data:

Select the Model tab on the Toolbar.
Select the Gradient Boosting node icon. Drag the node into the Diagram Workspace.
Connect the Control Point node to the Gradient Boosting node.
Select the Gradient Boosting node. In the Properties Panel, set the following properties:
- Click on the value for the Maximum Depth property, in the Splitting Rule subgroup, and enter 10. This property determines the number of generations in each decision tree created by the Gradient Boosting node.
- Click on the value for the Number of Surrogate Rules property, in the Node subgroup, and enter 2. Surrogate rules are backup rules that are used in the event of missing data. For example, if your primary splitting rule sorts donors based on their ZIP codes, then a reasonable surrogate rule would sort based on the donor’s city of residence.
In the Diagram Workspace, right-click the Gradient Boosting node, and select Run from the resulting menu. Click Yes in the Confirmation window that opens.
In the Run Status window, select OK.

Tip

The book “Decision Trees for Analytics Using SAS Enterprise Miner” offers additional information about alternative measures of the effectiveness of a split, options for training and pruning, suggestions for guiding tree growth, and examples of multiple tree and gradient boosting models.

Tip

“Predictive Modeling with SAS Enterprise Miner: Practical Solutions for Business Applications” offers examples that automatically and interactively train and prune decision tree models and examples that create gradient boosting models.