Usage Note 24516: What does the ANOVAF option in the PROC MIXED statement do?
 |  |  |  |
The ANOVAF option in the PROC MIXED statement computes F-tests by the following method:
Let L denote the matrix of estimable functions for
the hypothesis H: L[b'
g' ]' = 0, where b and g
are the fixed and random effects, respectively. Let M = L'(LL')–L
and suppose C denotes the estimated variance-covariance matrix of 
(see the section "Statistical
Properties" in the PROC MIXED documentation for the construction of C).
The ANOVAF F-statistics are computed as
Notice that this is a
modification of the usual F-statistic where 
is replaced with 
and rank(L) is
replaced with 
.
See, for example, Brunner, Domhof, and Langer (2002, Sec. 5.4). The p-values
for this statistic are computed from either an 
or an 
distribution. The respective degrees of
freedom are determined by the MIXED procedure as follows:
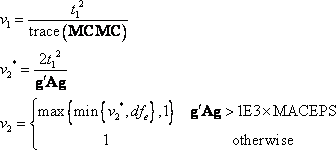
The term g'Ag in the term 
for the denominator degrees of
freedom is based on approximating Var[trace(MC)] based on a first-order Taylor
series about the true covariance parameters. This generalizes results in the
appendix of Brunner, Dette, and Munk (1997) to a broader class of models. The
vector g = [g1 ,…,gq]
contains the partial derivatives
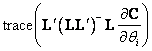
and A is the asymptotic variance-covariance matrix of the covariance parameter estimates (ASYCOV option in the PROC MIXED statement).
PROC MIXED reports n1
and n2 as NumDF and DenDF
under the ANOVA F heading in the output. The corresponding p-values are
denoted as Pr > F(DDF) for and Pr > F(infty)
for ,
respectively.
P-values that are computed with the ANOVAF option can be identical to the nonparametric tests in Akritas, Arnold, and Brunner (1997) and in Brunner, Domhof, and Langer (2002), provided the response data consists of properly created (and sorted) ranks and the covariance parameters are estimated by MIVQUE0 in models with the REPEATED statement and properly chosen SUBJECT= and/or GROUP= effects.
References
Akritas, M. G., S. F. Arnold, and E. Brunner. 1997. “Nonparametric Hypotheses and Rank Statistics for Unbalanced Factorial Designs.” Journal of the American Statistical Association 92:258–265.
Brunner, E., H. Dette, and A. Munk. 1997. “Box-Type Approximations in Nonparametric Factorial Designs.” Journal of the American Statistical Association 92:1494–1502.
Brunner, E., S. Domhof, and F. Langer. 2002. Nonparametric Analysis of Longitudinal Data in Factorial Experiments. New York: John Wiley & Sons, Inc.
Operating System and Release Information
| Product Family | Product | System | SAS Release | |
| Reported | Fixed* | |||
| SAS System | SAS/STAT | All | n/a | |
| Type: | Usage Note |
| Priority: | low |
| Topic: | SAS Reference ==> Procedures ==> MIXED Analytics ==> Mixed Models |
| Date Modified: | 2016-11-16 11:38:29 |
| Date Created: | 2006-07-05 16:58:30 |