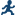Two-Sample t Test
About the Two-Sample t Test Task
A two-sample t test
compares the mean of the first sample minus the mean of the second
sample to a given number, the null hypothesis difference.
To compare means from
two independent samples with n1 and n2 observations
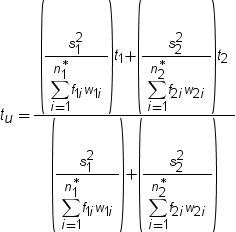
to a value m, use 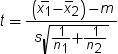 . In this example, s2 is
the pooled variance
. In this example, s2 is
the pooled variance 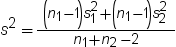 , and s21 and s22 are
the sample variances of the two groups. The use of this t statistic
depends on the assumption that
, and s21 and s22 are
the sample variances of the two groups. The use of this t statistic
depends on the assumption that 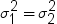 , where
, where 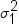 and
and 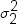 are the population variances of the two groups.
are the population variances of the two groups.
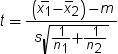 . In this example, s2 is
the pooled variance
. In this example, s2 is
the pooled variance 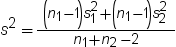 , and s21 and s22 are
the sample variances of the two groups. The use of this t statistic
depends on the assumption that
, and s21 and s22 are
the sample variances of the two groups. The use of this t statistic
depends on the assumption that 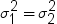 , where
, where 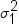 and
and 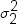 are the population variances of the two groups.
are the population variances of the two groups.
To run a two-sample t test,
open the t Tests task. From the t test drop-down
list, select Two-sample test.
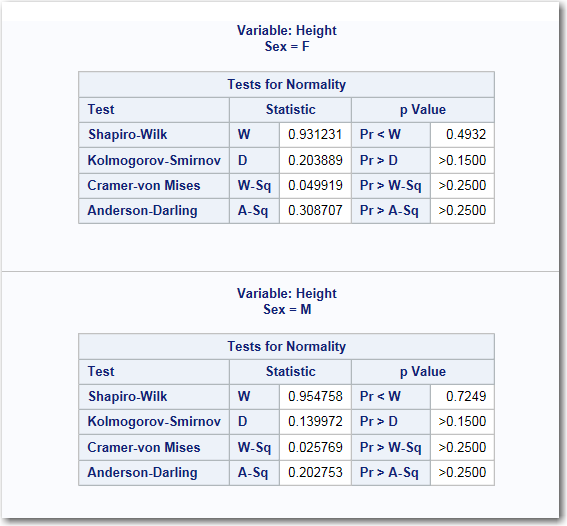
Example: Two-Sample t Test
In this example, you
want to analyze the height values for males and females in your class.
To create this example:
-
TipIf the data set is not available from the drop-down list, click
 . In the Choose a Table window,
expand the library that contains the data set that you want to use.
Select the data set for the example and click OK.
The selected data set should now appear in the drop-down list.
. In the Choose a Table window,
expand the library that contains the data set that you want to use.
Select the data set for the example and click OK.
The selected data set should now appear in the drop-down list.
Setting Options
Copyright © SAS Institute Inc. All rights reserved.