The SURVEYFREQ Procedure
Totals
PROC SURVEYFREQ estimates population frequency totals for the specified crosstabulation tables, including totals for two-way table cells, rows, columns, and overall totals. The procedure computes the estimate of the total frequency in table cell (r, c) as the weighted frequency sum,
![\[ \widehat{N}_{rc} = \sum _{h=1}^ H ~ \sum _{i=1}^{n_ h} ~ \sum _{j=1}^{m_{hi}} ~ {\delta _{hij} (r,c) ~ W_{hij}} \]](images/statug_surveyfreq0028.png)
Similarly, PROC SURVEYFREQ computes estimates of row totals, column totals, and overall totals as
![\[ \widehat{N}_{r \cdot } = \sum _{h=1}^ H ~ \sum _{i=1}^{n_ h} ~ \sum _{j=1}^{m_{hi}} ~ {\delta _{hij} (r ~ \cdot ) ~ W_{hij}} \]](images/statug_surveyfreq0029.png)
![\[ \widehat{N}_{\cdot c} = \sum _{h=1}^ H ~ \sum _{i=1}^{n_ h} ~ \sum _{j=1}^{m_{hi}} ~ {\delta _{hij} (\cdot ~ c) ~ W_{hij}} \]](images/statug_surveyfreq0030.png)
![\[ \widehat{N} ~ ~ = \sum _{h=1}^ H ~ \sum _{i=1}^{n_ h} ~ \sum _{j=1}^{m_{hi}} ~ {W_{hij}} \]](images/statug_surveyfreq0031.png)
PROC SURVEYFREQ estimates the variances of totals by using the variance estimation method that you request. If you request BRR variance estimation (by specifying the VARMETHOD=BRR option in the PROC SURVEYFREQ statement), the procedure estimates the variances as described in the section Balanced Repeated Replication (BRR). If you request jackknife variance estimation (by specifying the VARMETHOD=JACKKNIFE option), the procedure estimates the variances as described in the section The Jackknife Method.
If you do not specify the VARMETHOD= option or a REPWEIGHTS statement, the default variance estimation method is Taylor series, which you can also request by specifying the VARMETHOD=TAYLOR option. Because totals are linear statistics, their variances can be estimated directly, without the approximation that is used for proportions and other nonlinear statistics. PROC SURVEYFREQ estimates the variance of the total frequency in table cell (r, c) as
![\[ \widehat{\mr{Var}}(\widehat{N}_{rc}) = \sum _{h=1}^ H \widehat{\mr{Var}}_ h(\widehat{N}_{rc}) \]](images/statug_surveyfreq0032.png)
where if 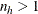 ,
,
![\begin{eqnarray*} \widehat{\mr{Var}}_ h(\widehat{N}_{rc}) & =& \frac{n_ h(1-f_ h)}{n_ h-1} ~ \sum _{i=1}^{n_ h} {(n_{rc}^{~ hi} - \bar{n}_{rc}^{~ h})^2 } \\ n_{rc}^{~ hi} & =& \sum _{j=1}^{m_{hi}} ~ {\delta _{hij} (r,c) ~ W_{hij}} \\[0.1in] \bar{n}_{rc}^{~ h} & =& \left( \sum _{i=1}^{n_ h} ~ {n_{rc}^{~ hi}} \right) ~ / ~ n_ h \end{eqnarray*}](images/statug_surveyfreq0034.png)
and if 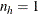 ,
,
![\[ \widehat{\mr{Var}}_ h(\widehat{N}_{rc}) = \left\{ \begin{array}{ll} \mr{missing} & \mbox{ if } n_{h'}=1 \mbox{ for } h’=1, 2, \ldots , H \\ 0 & \mbox{ if } n_{h'}>1 \mbox{ for some } 1 \leq h’ \leq H \end{array} \right. \]](images/statug_surveyfreq0036.png)
The standard deviation of the total is computed as
![\[ \mr{Std}( \widehat{N}_{rc} ) = \sqrt { \widehat{\mr{Var}}( \widehat{N}_{rc} ) } \]](images/statug_surveyfreq0037.png)
The variances and standard deviations are computed in a similar manner for row totals, column totals, and overall table totals.
