Introduction to Survival Analysis Procedures

Cox Regression and Extensions: The PHREG Procedure

The PHREG procedure fits the proportional hazards model of Cox (1972, 1975) to survival data that might be right-censored. The Cox model is a semiparametric model in which the hazard function of the survival time is given by

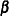$\lambda (t;\mb{x}) = \lambda _0(t) \mr{e}^{\bbeta ^{\prime }\mb{x}(t)}$

where $\lambda _0(t)$ is an unspecified baseline hazard function, $\mb{x}(t)$ is a vector of covariate values (possibly time-dependent), and $\bbeta$ is a vector of unknown regression parameters. The model is referred to as a semiparametric model, because part of the model involves the unspecified baseline function over time (which has an infinite dimension) and the other part involves a finite number of regression parameters. Texts that discuss the Cox regression models include Collett (1994); Cox and Oakes (1984); Kalbfleisch and Prentice (1980); Lawless (1982). Extensions of the Cox model are discussed in Therneau and Grambsch (2000); Andersen et al. (1992); Fleming and Harrington (1991); Fine and Gray (1999). For more information about PROC PHREG, see Chapter 85: The PHREG Procedure.