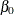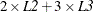The Four Types of Estimable Functions
Examples
A One-Way Classification Model
For the model
![\[ Y = \mu + A_ i + \epsilon \quad \quad i = 1, 2, 3 \]](images/statug_introglmest0038.png)
the general form of estimable functions 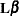 is (from the previous example)
is (from the previous example)
![\[ \mb{L} \bbeta = \mathit{L1} \times \mu + \mathit{L2} \times A_1 + \mathit{L3} \times A_2 + (\mathit{L1}-\mathit{L2}-\mathit{L3}) \times A_3 ~ \]](images/statug_introglmest0039.png)
Thus,
![\[ \mb{L} = (\mathit{L1}, \mathit{L2}, \mathit{L3}, \mathit{L1}-\mathit{L2}-\mathit{L3}) \]](images/statug_introglmest0040.png)
Tests involving only the parameters 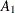 ,
, 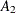 , and
, and 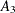 must have an
must have an  of the form
of the form
![\[ \mb{L} = (0, \mathit{L2}, \mathit{L3}, -\mathit{L2}-\mathit{L3}) ~ \]](images/statug_introglmest0044.png)
Since this  for the A parameters involves only two symbols, hypotheses with at most two degrees of freedom can be constructed. For example, letting
for the A parameters involves only two symbols, hypotheses with at most two degrees of freedom can be constructed. For example, letting
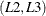 be
be 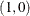 and
and 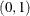 , respectively, yields
, respectively, yields
![\[ \mb{L} = \left[ \begin{array}{rrrr} 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & -1 \end{array} \right] \]](images/statug_introglmest0048.png)
The preceding  can be used to test the hypothesis that
can be used to test the hypothesis that 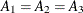 . For this example, any
. For this example, any  with two linearly independent rows with column 1 equal to zero produces the same sum of squares. For example, a joint test
for linear and quadratic effects of A
with two linearly independent rows with column 1 equal to zero produces the same sum of squares. For example, a joint test
for linear and quadratic effects of A
![\[ \mb{L} = \left[ \begin{array}{rrrr} 0 & 1 & 0 & -1 \\ 0 & 1 & -2 & 1 \end{array} \right] \]](images/statug_introglmest0050.png)
gives the same SS. In fact, for any  of full row rank and any nonsingular matrix
of full row rank and any nonsingular matrix 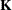 of conformable dimensions,
of conformable dimensions,
![\[ \mbox{SS}(H_0\colon ~ \mb{L} \bbeta = 0) = \mbox{SS}(H_0\colon ~ \mb{KL} \bbeta = 0) ~ \]](images/statug_introglmest0051.png)
A Three-Factor Main-Effects Model
Consider a three-factor main-effects model involving the CLASS variables A, B, and C, as shown in Table 15.1.
Table 15.1: Three-Factor Main-Effects Model
|
Obs |
A |
B |
C |
|||
|---|---|---|---|---|---|---|
|
1 |
1 |
2 |
1 |
|||
|
2 |
1 |
1 |
2 |
|||
|
3 |
2 |
1 |
3 |
|||
|
4 |
2 |
2 |
2 |
|||
|
5 |
2 |
2 |
2 |
The general form of an estimable function is shown in Table 15.2.
Table 15.2: General Form of an Estimable Function for Three-Factor Main-Effects Model
|
Parameter |
Coefficient |
|
|---|---|---|
|
|
L1 |
|
|
A1 |
L2 |
|
|
A2 |
L1 – L2 |
|
|
B1 |
L4 |
|
|
B2 |
L1 – L4 |
|
|
C1 |
L6 |
|
|
C2 |
L1 + L2 – L4 – 2 |
|
|
C3 |
–L2 + L4 + L6 |
Since only four symbols (L1, L2, L4, and L6) are involved, any testable hypothesis will have at most four degrees of freedom. If you form an  matrix with four linearly independent rows according to the preceding rules, then testing
matrix with four linearly independent rows according to the preceding rules, then testing 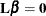 is equivalent to testing that
is equivalent to testing that ![$\mr{E}[\mb{Y}]$](images/statug_introglmest0054.png) is uniformly 0. Symbolically,
is uniformly 0. Symbolically,
![\[ \mbox{SS}(H_0\colon ~ \mb{L} \bbeta = 0) = R(\mu , A, B, C) ~ \]](images/statug_introglmest0055.png)
In a main-effects model, the usual hypothesis of interest for a main effect is the equality of all the parameters. In this example, it is not possible to unambiguously test such a hypothesis because of confounding: any test for the equality of the parameters for any one of A, B, or C will necessarily involve the parameters for the other two effects. One way to proceed is to construct a maximum rank hypothesis (MRH) involving only the parameters of the main effect in question. This can be done using the general form of estimable functions. Note the following:
-
To get an MRH involving only the parameters of A, the coefficients of
 associated with
associated with 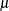 , B1, B2, C1, C2, and C3 must be equated to zero. Starting at the top of the general form, let L1 = 0, then L4 = 0, then L6 = 0. If C2 and C3 are not to be involved, then L2 must also be zero. Thus, A1 – A2 is not estimable; that is, the MRH involving only the A parameters has zero rank and
, B1, B2, C1, C2, and C3 must be equated to zero. Starting at the top of the general form, let L1 = 0, then L4 = 0, then L6 = 0. If C2 and C3 are not to be involved, then L2 must also be zero. Thus, A1 – A2 is not estimable; that is, the MRH involving only the A parameters has zero rank and 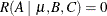 .
.
-
To obtain the MRH involving only the B parameters, let L1 = L2 = L6 = 0. But then to remove C2 and C3 from the comparison, L4 must also be set to 0. Thus, B1 – B2 is not estimable and
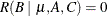 .
.
-
To obtain the MRH involving only the C parameters, let L1 = L2 = L4 =0. Thus, the MRH involving only C parameters is
![\[ \mathit{C1} - 2 \times \mathit{C2} +\mathit{C3} = K \quad \quad \mbox{(for any } K\text {)} \]](images/statug_introglmest0058.png)
or any multiple of the left-hand side equal to K. Furthermore,
![\[ \mbox{SS}(H_0\colon ~ \mathit{C1} - 2 \times \mathit{C2} + \mathit{C3} = 0) = R(C~ |~ \mu , A, B) \]](images/statug_introglmest0059.png)
A Multiple Regression Model
Suppose
![\[ \mr{E}[Y] = \beta _0 + \beta _1 x_1 + \beta _2 x_2 + \beta _3 x_3 \]](images/statug_introglmest0060.png)
where the 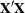 matrix has full rank. The general form of estimable functions is as shown in Table 15.3.
matrix has full rank. The general form of estimable functions is as shown in Table 15.3.
Table 15.3: General Form of Estimable Functions for a Multiple Regression Model When 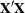 Matrix Is of Full Rank
Matrix Is of Full Rank
|
Parameter |
Coefficient |
|
|---|---|---|
|
|
L1 |
|
|
|
L2 |
|
|
|
L3 |
|
|
|
L4 |
For example, to test the hypothesis that 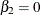 , let L1 = L2 = L4 = 0 and let L3 = 1. Then SS
, let L1 = L2 = L4 = 0 and let L3 = 1. Then SS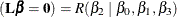 . In this full-rank case, all parameters, as well as any linear combination of parameters, are estimable.
. In this full-rank case, all parameters, as well as any linear combination of parameters, are estimable.
Suppose, however, that 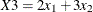 . The general form of estimable functions is shown in Table 15.4.
. The general form of estimable functions is shown in Table 15.4.
Table 15.4: General Form of Estimable Functions for a Multiple Regression Model When 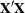 Matrix Is Not of Full Rank
Matrix Is Not of Full Rank
|
Parameter |
Coefficient |
|
|---|---|---|
|
|
L1 |
|
|
|
L2 |
|
|
|
L3 |
|
|
|
|
For this example, it is possible to test 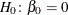 . However,
. However, 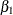 ,
, 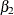 , and
, and 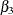 are not jointly estimable; that is,
are not jointly estimable; that is,
![\begin{eqnarray*} R(\beta _1~ |~ \beta _0, \beta _2, \beta _3) & = & 0 \\[0.05in] R(\beta _2~ |~ \beta _0, \beta _1, \beta _3) & = & 0 \\[0.05in] R(\beta _3~ |~ \beta _0, \beta _1, \beta _2) & = & 0 ~ \end{eqnarray*}](images/statug_introglmest0070.png)