Introduction to Structural Equation Modeling with Latent Variables
The Structural Model
The last component of the LISMOD specification is the structural model that describes the relationship between 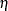 and
and 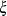 , as shown in the following equation:
, as shown in the following equation:
![\[ \eta = \bbeta \eta + \bGamma \xi + \zeta \]](images/statug_introcalis0064.png)
In this equation, 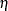 is endogenous (dependent) and
is endogenous (dependent) and 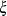 is exogenous (independent). Variables in
is exogenous (independent). Variables in 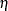 can have effects among themselves. Their effects are specified in the
can have effects among themselves. Their effects are specified in the 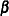 matrix. The effects of
matrix. The effects of 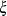 on
on 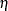 are specified in the
are specified in the  matrix. Finally, the error term for the structural relationships is denoted by
matrix. Finally, the error term for the structural relationships is denoted by 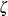 , which is independent of
, which is independent of 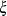 .
.
There are four model matrices assumed in the structural model. 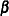 and
and  are matrices for the effects of variables. In addition, matrix
are matrices for the effects of variables. In addition, matrix 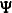 denotes the covariance matrix for the error term
denotes the covariance matrix for the error term 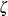 , and matrix
, and matrix 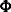 denotes the covariance matrix of
denotes the covariance matrix of 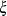 .
.
For the career aspiration data, you use the following MATRIX statements for the structural model:
matrix _beta_ [2,1],[1,2]; matrix _gamma_ [1,1 to 4], [2,3 to 6]; matrix _psi_ [2,1]; matrix _phi_ [1,1] = 6 * 1.0;
In Figure 17.52, initial _BETA_ and _GAMMA_ matrices are shown.
Figure 17.52: Career Aspiration Analysis 3: Initial Structural Equations
In Figure 17.52, the _BETA_ matrix contains information about the relationships among the 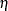 -variables (ETA= variables). Both the row and column variables of the _BETA_ matrix refer to the list of
-variables (ETA= variables). Both the row and column variables of the _BETA_ matrix refer to the list of 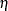 -variables. The row variables receive effects from the column variables. You specify two parameters in the _BETA_ matrix:
element [2,1] is the effect of
-variables. The row variables receive effects from the column variables. You specify two parameters in the _BETA_ matrix:
element [2,1] is the effect of R_Amb on F_Amb, and element [2,1] is the effect of F_Amb on R_Amb. Other effects are fixed zeros in this matrix.
The _GAMMA_ matrix contains information about the relationships between the 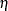 -variables (ETA= variables) and the
-variables (ETA= variables) and the 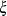 -variables (XI= variables). The row variables are the
-variables (XI= variables). The row variables are the 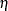 -variables, which receive effects from the column
-variables, which receive effects from the column 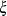 -variables. You specify eight free parameters in this matrix. These eight parameters represent the eight path coefficients
from
-variables. You specify eight free parameters in this matrix. These eight parameters represent the eight path coefficients
from 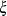 (the intelligence and environment factors) to the
(the intelligence and environment factors) to the 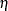 variables (the ambition factors), as shown in the path diagram in Figure 17.47. A shortcut in the MATRIX statement syntax for the _GAMMA_ matrix has been used. That is,
variables (the ambition factors), as shown in the path diagram in Figure 17.47. A shortcut in the MATRIX statement syntax for the _GAMMA_ matrix has been used. That is, [1, 1 to 4] means the [1,1], [1,2], [1,3], and [1,4] elements, and [2, 3 to 6] means the [2,3], [2,4], [2,5], and [2,6] elements. All these elements are free parameters in the model and free parameter
names are generated for these elements.
Figure 17.53 shows the initial _PSI_ and _PHI_ matrices.
Figure 17.53: Career Aspiration Analysis 3: Initial Variances and Covariances
| Initial _PHI_ Matrix | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f_rpa | f_riq | f_rses | f_fses | f_fiq | f_fpa | |||||||||||||
| f_rpa |
|
|
|
|
|
|
||||||||||||
| f_riq |
|
|
|
|
|
|
||||||||||||
| f_rses |
|
|
|
|
|
|
||||||||||||
| f_fses |
|
|
|
|
|
|
||||||||||||
| f_fiq |
|
|
|
|
|
|
||||||||||||
| f_fpa |
|
|
|
|
|
|
||||||||||||
| NOTE: Parameters with prefix '_Add' are added by PROC CALIS. | ||||||||||||||||||
The _PSI_ matrix contains information about the covariances of error terms for the 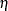 -variables, which are endogenous in the structural model. There are two
-variables, which are endogenous in the structural model. There are two 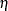 -variables in the model—the two ambition factors
-variables in the model—the two ambition factors R_Amb and F_Amb. You specify the [2,1] element as a free parameter in the MATRIX statement for _PSI_. This means that the error covariance
between R_Amb and F_Amb is a free parameter to estimate in the model. In Figure 17.53, both [2,1] and [1,2] elements are named as _Parm15 because _PSI_ is a symmetric matrix. Again, the diagonal elements of this covariance matrix, which are for the error variances
of the ambition factors, are default free parameters in PROC CALIS. These parameters are named with the prefix _Add.
Finally, the _PHI_ matrix contains information about the covariances among the exogenous latent factors in the structural model. For the _PHI_ matrix, you fix all the diagonal elements to 1 in the MATRIX statement for _PHI_. This makes the latent variable scales identified. These fixed values are echoed in the output of the initial _PHI_ matrix shown in Figure 17.53. In addition, all covariances among latent exogenous variables are set to be free parameters by default.