The HPPRINCOMP Procedure
ITERGS
The iterative method based on Gram-Schmidt orthogonalization (ITERGS) of Andrecut (2009) overcomes the issue of loss of orthogonality in the NIPALS method by applying Gram-Schmidt reorthogonalization correction to both the loadings and the scores at each iteration step:
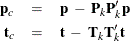
Here, 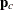 and
and 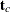 are the corrected loading vector and score vector, respectively.
are the corrected loading vector and score vector, respectively. 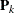 is the matrix that is formed by using the first k loadings.
is the matrix that is formed by using the first k loadings. 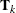 is the matrix that is formed by using the first k scores.
is the matrix that is formed by using the first k scores.
The ITERGS method stabilizes the iterative process at the cost of increased computational effort.
