The GLIMMIX Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function -
Details
 Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics -
Examples
 Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model - References
Scale and Dispersion Parameters
The parameter  in the log-likelihood functions is a scale parameter. McCullagh and Nelder (1989, p. 29) refer to it as the
dispersion parameter. With the exception of the normal distribution,
in the log-likelihood functions is a scale parameter. McCullagh and Nelder (1989, p. 29) refer to it as the
dispersion parameter. With the exception of the normal distribution,  does not correspond to the variance of an observation, the variance of an observation in a generalized linear model is a
function of
does not correspond to the variance of an observation, the variance of an observation in a generalized linear model is a
function of  and
and 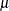 . In a generalized linear model
(GLM mode), the GLIMMIX procedure displays the estimate of
. In a generalized linear model
(GLM mode), the GLIMMIX procedure displays the estimate of  is as "Scale" in the "Parameter Estimates" table. Note that for some distributions this scale is different from that reported
by the GENMOD procedure in its "Parameter Estimates" table. The scale reported by PROC GENMOD is sometimes a transformation
of the dispersion parameter in the log-likelihood function. Table 45.21 displays the relationship between the "Scale" entries reported by the two procedures in terms of the
is as "Scale" in the "Parameter Estimates" table. Note that for some distributions this scale is different from that reported
by the GENMOD procedure in its "Parameter Estimates" table. The scale reported by PROC GENMOD is sometimes a transformation
of the dispersion parameter in the log-likelihood function. Table 45.21 displays the relationship between the "Scale" entries reported by the two procedures in terms of the  (or k) parameter in the GLIMMIX log-likelihood functions.
(or k) parameter in the GLIMMIX log-likelihood functions.
Table 45.21: Scales in Parameter Estimates Table
|
Distribution |
GLIMMIX Reports |
GENMOD Reports |
|---|---|---|
|
Beta |
|
N/A |
|
Gamma |
|
|
|
Inverse Gaussian |
|
|
|
Negative binomial |
|
|
|
Normal |
|
|
Note that for normal linear models, PROC GLIMMIX by default estimates the parameters by restricted maximum likelihood, whereas PROC GENMOD estimates the parameters by maximum likelihood. As a consequence, the scale parameter in the "Parameter Estimates" table of the GLIMMIX procedure coincides for these models with the mean-squared error estimate of the GLM or REG procedures. To obtain maximum likelihood estimates in a normal linear model in the GLIMMIX procedure, specify the NOREML option in the PROC GLIMMIX statement.
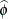
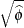
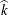
![$\widehat{\phi } = \widehat{\mr{Var}}[Y]$](images/statug_glimmix0545.png)