The FREQ Procedure
Binomial Proportion
If you specify the BINOMIAL option in the TABLES statement, PROC FREQ computes the binomial proportion for one-way tables. By default, this is the proportion of observations in the first variable level that appears in the output. (You can use the LEVEL= option to specify a different level for the proportion.) The binomial proportion is computed as
![\[ \hat{p} = n_{1} ~ / ~ n \]](images/statug_freq0183.png)
where 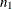 is the frequency of the first (or designated) level and n is the total frequency of the one-way table. The standard error of the binomial proportion is computed as
is the frequency of the first (or designated) level and n is the total frequency of the one-way table. The standard error of the binomial proportion is computed as
![\[ \mr{se}(\hat{p}) = \sqrt { \hat{p} ~ (1 - \hat{p} ) ~ / ~ n } \]](images/statug_freq0185.png)
Binomial Confidence Limits
PROC FREQ provides Wald and exact (Clopper-Pearson) confidence limits for the binomial proportion. You can also request the following binomial confidence limit types by specifying the BINOMIAL(CL=) option: Agresti-Coull, Blaker, Jeffreys, exact mid-p, likelihood ratio, logit, and Wilson (score). For more information, see Brown, Cai, and DasGupta (2001), Agresti and Coull (1998), and Newcombe (1998b), in addition to the references cited for each confidence limit type.
Wald Confidence Limits
Wald asymptotic confidence limits are based on the normal approximation to the binomial distribution. PROC FREQ computes the Wald confidence limits for the binomial proportion as
![\[ \hat{p} ~ \pm ~ ( ~ z_{\alpha /2} \times \mr{se}(\hat{p}) ~ ) \]](images/statug_freq0186.png)
where 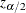 is the
is the 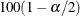 th percentile of the standard normal distribution. The confidence level
th percentile of the standard normal distribution. The confidence level  is determined by the ALPHA= option; by default, ALPHA=0.05, which produces 95% confidence limits.
is determined by the ALPHA= option; by default, ALPHA=0.05, which produces 95% confidence limits.
If you specify CL=WALD(CORRECT) or the CORRECT binomial-option, PROC FREQ includes a continuity correction of 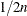 in the Wald asymptotic confidence limits. The purpose of this correction is to adjust for the difference between the normal
approximation and the discrete binomial distribution. See Fleiss, Levin, and Paik (2003) for more information. The continuity-corrected Wald confidence limits for the binomial proportion are computed as
in the Wald asymptotic confidence limits. The purpose of this correction is to adjust for the difference between the normal
approximation and the discrete binomial distribution. See Fleiss, Levin, and Paik (2003) for more information. The continuity-corrected Wald confidence limits for the binomial proportion are computed as
![\[ \hat{p} ~ \pm ~ ( ~ z_{\alpha /2} \times \mr{se}(\hat{p}) ~ + ~ (1/2n) ~ ) \]](images/statug_freq0188.png)
Exact (Clopper-Pearson) Confidence Limits
Exact (Clopper-Pearson) confidence limits for the binomial proportion are constructed by inverting the equal-tailed test based
on the binomial distribution. This method is attributed to Clopper and Pearson (1934). The exact confidence limits 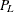 and
and 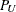 satisfy the following equations, for
satisfy the following equations, for 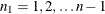 :
:
![\begin{eqnarray*} \sum _{x=n_1}^{n} \binom {n}{x} P_{\mi{L}}^{~ x} (1 - P_{\mi{L}})^{~ n-x} & = & \alpha /2 \\[0.1in] \sum _{x=0}^{n_1} \binom {n}{x} P_{\mi{U}}^{~ x} (1 - P_{\mi{U}})^{~ n-x} & = & \alpha /2 \end{eqnarray*}](images/statug_freq0192.png)
The lower confidence limit is 0 when 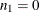 , and the upper confidence limit is 1 when
, and the upper confidence limit is 1 when 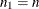 .
.
PROC FREQ computes the exact (Clopper-Pearson) confidence limits by using the F distribution as
![\[ P_{\mi{L}} = \left( 1 + \frac{n - n_1 + 1}{n_1 ~ F(~ \alpha /2, ~ 2 n_1,~ 2(n - n_1 + 1) ~ )} \right)^{-1} \]](images/statug_freq0195.png)
![\[ P_{\mi{U}} = \left( 1 + \frac{n - n_1}{(n_1 + 1) ~ F(~ 1-\alpha /2, ~ 2(n_1 + 1), ~ 2(n - n_1) ~ )} \right)^{-1} \]](images/statug_freq0196.png)
where 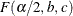 is the (
is the (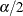 )th percentile of the F distribution with b and c degrees of freedom. See Leemis and Trivedi (1996) for a derivation of this expression. Also see Collett (1991) for more information about exact binomial confidence limits.
)th percentile of the F distribution with b and c degrees of freedom. See Leemis and Trivedi (1996) for a derivation of this expression. Also see Collett (1991) for more information about exact binomial confidence limits.
Because this is a discrete problem, the confidence coefficient (coverage probability) of the exact (Clopper-Pearson) interval
is not exactly 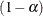 but is at least
but is at least 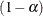 . Thus, this confidence interval is conservative. Unless the sample size is large, the actual coverage probability can be
much larger than the target value. For more information about the performance of these confidence limits, see Agresti and
Coull (1998), Brown, Cai, and DasGupta (2001), and Leemis and Trivedi (1996).
. Thus, this confidence interval is conservative. Unless the sample size is large, the actual coverage probability can be
much larger than the target value. For more information about the performance of these confidence limits, see Agresti and
Coull (1998), Brown, Cai, and DasGupta (2001), and Leemis and Trivedi (1996).
Agresti-Coull Confidence Limits
If you specify the CL=AGRESTICOULL binomial-option, PROC FREQ computes Agresti-Coull confidence limits for the binomial proportion as
![\[ \tilde{p} ~ \pm ~ ( ~ z_{\alpha /2} \times \sqrt { \tilde{p} ~ (1-\tilde{p}) ~ / ~ \tilde{n} } ~ ) \]](images/statug_freq0200.png)
where
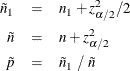
The Agresti-Coull confidence interval has the same general form as the standard Wald interval but uses 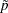 in place of
in place of 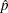 . For
. For 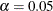 , the value of
, the value of 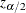 is close to 2, and this interval is the "add 2 successes and 2 failures" adjusted Wald interval of Agresti and Coull (1998).
is close to 2, and this interval is the "add 2 successes and 2 failures" adjusted Wald interval of Agresti and Coull (1998).
Blaker Confidence Limits
If you specify the CL=BLAKER binomial-option, PROC FREQ computes Blaker confidence limits for the binomial proportion, which are constructed by inverting the two-sided
exact Blaker test (Blaker 2000). The 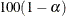 % Blaker confidence interval consists of all values of the proportion
% Blaker confidence interval consists of all values of the proportion 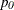 for which the test statistic
for which the test statistic 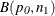 falls in the acceptance region,
falls in the acceptance region,
![\[ \{ p_{\mi{0}}: B(p_{\mi{0}}, n_1) > \alpha \} \]](images/statug_freq0206.png)
where
![\[ B( p_{\mi{0}}, n_1 ) ~ = ~ \mr{Prob}(~ \gamma (p_{\mi{0}}, X) \leq \gamma (p_{\mi{0}}, n_1)~ |~ p_{\mi{0}}~ ) \]](images/statug_freq0207.png)
![\[ \gamma ( p_{\mi{0}}, n_1 ) ~ = ~ \min (~ \mr{Prob}(~ X \geq n_1~ |~ p_{\mi{0}}~ ),~ \mr{Prob}(~ X \leq n_1~ |~ p_{\mi{0}}~ )~ ) \]](images/statug_freq0208.png)
and X is a binomial random variable. For more information, see Blaker (2000).
Jeffreys Confidence Limits
If you specify the CL=JEFFREYS binomial-option, PROC FREQ computes Jeffreys confidence limits for the binomial proportion as
![\[ \bigl ( ~ \beta ( \alpha /2, ~ n_1 + 1/2, ~ n - n_1 + 1/2 ), ~ ~ \beta ( 1-\alpha /2, ~ n_1 + 1/2, ~ n - n_1 + 1/2 ) ~ \bigr ) \]](images/statug_freq0209.png)
where 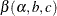 is the
is the  th percentile of the beta distribution with shape parameters b and c. The lower confidence limit is set to 0 when
th percentile of the beta distribution with shape parameters b and c. The lower confidence limit is set to 0 when 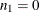 , and the upper confidence limit is set to 1 when
, and the upper confidence limit is set to 1 when 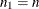 . This is an equal-tailed interval based on the noninformative Jeffreys prior for a binomial proportion. For more information,
see Brown, Cai, and DasGupta (2001). For information about using beta priors for inference on the binomial proportion, see Berger (1985).
. This is an equal-tailed interval based on the noninformative Jeffreys prior for a binomial proportion. For more information,
see Brown, Cai, and DasGupta (2001). For information about using beta priors for inference on the binomial proportion, see Berger (1985).
Likelihood Ratio Confidence Limits
If you specify the CL=LIKELIHOODRATIO binomial-option, PROC FREQ computes likelihood ratio confidence limits for the binomial proportion by inverting the likelihood ratio test.
The likelihood ratio test statistic for the null hypothesis that the proportion equals 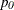 can be expressed as
can be expressed as
![\[ L(p_{\mi{0}}) ~ = ~ -2 \left( n_1 \log ( \hat{p} / p_{\mi{0}} ) ~ + ~ (n - n_1) \log ( (1-\hat{p}) / (1-p_{\mi{0}}) ) \right) \]](images/statug_freq0211.png)
The 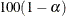 % likelihood ratio confidence interval consists of all values of
% likelihood ratio confidence interval consists of all values of 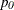 for which the test statistic
for which the test statistic 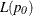 falls in the acceptance region,
falls in the acceptance region,
![\[ \{ p_{\mi{0}}: L( p_{\mi{0}} ) < \chi ^2_{1, \alpha } \} \]](images/statug_freq0213.png)
where 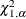 is the 100
is the 100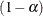 th percentile of the chi-square distribution with 1 degree of freedom. PROC FREQ finds the confidence limits by iterative
computation. For more information, see Fleiss, Levin, and Paik (2003), Brown, Cai, and DasGupta (2001), Agresti (2013), and Newcombe (1998b).
th percentile of the chi-square distribution with 1 degree of freedom. PROC FREQ finds the confidence limits by iterative
computation. For more information, see Fleiss, Levin, and Paik (2003), Brown, Cai, and DasGupta (2001), Agresti (2013), and Newcombe (1998b).
Logit Confidence Limits
If you specify the CL=LOGIT binomial-option, PROC FREQ computes logit confidence limits for the binomial proportion, which are based on the logit transformation 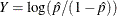 . Approximate confidence limits for Y are computed as
. Approximate confidence limits for Y are computed as
![\[ Y_{\mi{L}} ~ = ~ \log ( \hat{p}/(1-\hat{p}) ) ~ - ~ z_{\alpha /2} \sqrt { n / (n_1 (n-n_1)) } \]](images/statug_freq0216.png)
![\[ Y_{\mi{U}} ~ = ~ \log ( \hat{p}/(1-\hat{p}) ) ~ + ~ z_{\alpha /2} \sqrt { n / (n_1 (n-n_1)) } \]](images/statug_freq0217.png)
The confidence limits for Y are inverted to produce 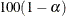 % logit confidence limits
% logit confidence limits 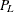 and
and 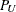 for the binomial proportion p as
for the binomial proportion p as
![\[ P_{\mi{L}} ~ = ~ \exp ( Y_{\mi{L}} / ( 1 + \exp ( Y_{\mi{L}} ) ) \]](images/statug_freq0218.png)
![\[ P_{\mi{U}} ~ = ~ \exp ( Y_{\mi{U}} / ( 1 + \exp ( Y_{\mi{U}} ) ) \]](images/statug_freq0219.png)
For more information, see Brown, Cai, and DasGupta (2001) and Korn and Graubard (1998).
Mid-p Confidence Limits
If you specify the CL=MIDP binomial-option, PROC FREQ computes exact mid-p confidence limits for the binomial proportion by inverting two one-sided binomial tests that include mid-p tail areas. The mid-p approach replaces the probability of the observed frequency by half of that probability in the Clopper-Pearson sum, which
is described in the section Exact (Clopper-Pearson) Confidence Limits. The exact mid-p confidence limits 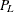 and
and 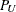 are the solutions to the equations
are the solutions to the equations
![\begin{eqnarray*} \sum _{x=n_1+1}^{n} \binom {n}{x} P_{\mi{L}}^{~ x} (1 - P_{\mi{L}})^{~ n-x} ~ + ~ \frac{1}{2} \binom {n}{n_1} P_{\mi{L}}^{~ n_1} (1 - P_{\mi{L}})^{~ n-n_1} & = & \alpha /2 \\[0.1in] \sum _{x=0}^{n_1-1} \binom {n}{x} P_{\mi{U}}^{~ x} (1 - P_{\mi{U}})^{~ n-x} ~ + ~ \frac{1}{2} \binom {n}{n_1} P_{\mi{U}}^{~ n_1} (1 - P_{\mi{U}})^{~ n-n_1} & = & \alpha /2 \end{eqnarray*}](images/statug_freq0220.png)
For more information, see Agresti and Gottard (2007), Agresti (2013), Newcombe (1998b), and Brown, Cai, and DasGupta (2001).
Wilson (Score) Confidence Limits
If you specify the CL=WILSON binomial-option, PROC FREQ computes Wilson confidence limits for the binomial proportion. These are also known as score confidence limits (Wilson 1927). The confidence limits are based on inverting the normal test that uses the null proportion in the variance (the score test). Wilson confidence limits are the roots of
![\[ | p - \hat{p} | = z_{\alpha /2} \sqrt { p (1-p)/n } \]](images/statug_freq0221.png)
and are computed as
![\[ \left( \hat{p} ~ + ~ z_{\alpha /2}^2/2n ~ \pm ~ z_{\alpha /2} \sqrt { \left( \hat{p} (1-\hat{p}) + z_{\alpha /2}^2 / 4n \right) / n } ~ \right) ~ / ~ \left( 1 + z_{\alpha /2}^2 / n \right) \]](images/statug_freq0222.png)
If you specify CL=WILSON(CORRECT) or the CORRECT binomial-option, PROC FREQ provides continuity-corrected Wilson confidence limits, which are computed as the roots of
![\[ | p - \hat{p} | - 1/2n = z_{\alpha /2} \sqrt { p (1-p)/n } \]](images/statug_freq0223.png)
The Wilson interval has been shown to have better performance than the Wald interval and the exact (Clopper-Pearson) interval. For more information, see Agresti and Coull (1998), Brown, Cai, and DasGupta (2001), and Newcombe (1998b).
Binomial Tests
The BINOMIAL option provides an asymptotic equality test for the binomial proportion by default. You can also specify binomial-options to request tests of noninferiority, superiority, and equivalence for the binomial proportion. If you specify the BINOMIAL option in the EXACT statement, PROC FREQ also computes exact p-values for the tests that you request with the binomial-options.
Equality Test
PROC FREQ computes an asymptotic test of the hypothesis that the binomial proportion equals 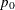 , where you can specify the value of
, where you can specify the value of 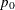 with the P= binomial-option. If you do not specify a null value with P=, PROC FREQ uses
with the P= binomial-option. If you do not specify a null value with P=, PROC FREQ uses 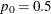 by default. The binomial test statistic is computed as
by default. The binomial test statistic is computed as
![\[ z = ( \hat{p} - p_0 ) / \mr{se} \]](images/statug_freq0226.png)
By default, the standard error is based on the null hypothesis proportion as
![\[ \mr{se} = \sqrt { p_0 ( 1 - p_0 ) / n} \]](images/statug_freq0227.png)
If you specify the VAR=SAMPLE binomial-option, the standard error is computed from the sample proportion as
![\[ \mr{se} = \sqrt { \hat{p} ( 1 - \hat{p} ) / n } \]](images/statug_freq0228.png)
If you specify the CORRECT binomial-option, PROC FREQ includes a continuity correction in the asymptotic test statistic, towards adjusting for the difference between
the normal approximation and the discrete binomial distribution. For more information, see Fleiss, Levin, and Paik (2003). The continuity correction of 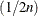 is subtracted from the numerator of the test statistic if
is subtracted from the numerator of the test statistic if 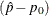 is positive; otherwise, the continuity correction is added to the numerator.
is positive; otherwise, the continuity correction is added to the numerator.
PROC FREQ computes one-sided and two-sided p-values for this test. When the test statistic z is greater than 0 (its expected value under the null hypothesis), PROC FREQ computes the right-sided p-value, which is the probability of a larger value of the statistic occurring under the null hypothesis. A small right-sided
p-value supports the alternative hypothesis that the true value of the proportion is greater than 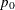 . When the test statistic is less than or equal to 0, PROC FREQ computes the left-sided p-value, which is the probability of a smaller value of the statistic occurring under the null hypothesis. A small left-sided
p-value supports the alternative hypothesis that the true value of the proportion is less than
. When the test statistic is less than or equal to 0, PROC FREQ computes the left-sided p-value, which is the probability of a smaller value of the statistic occurring under the null hypothesis. A small left-sided
p-value supports the alternative hypothesis that the true value of the proportion is less than 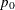 . The one-sided p-value
. The one-sided p-value 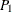 can be expressed as
can be expressed as
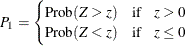
where Z has a standard normal distribution. The two-sided p-value is computed as 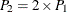 .
.
If you specify the BINOMIAL option in the EXACT
statement, PROC FREQ also computes an exact test of the null hypothesis 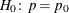 . To compute the exact test, PROC FREQ uses the binomial probability function,
. To compute the exact test, PROC FREQ uses the binomial probability function,
![\[ \mr{Prob} (X = x ~ | ~ p_0 ) = \binom {n}{x} p_0^{~ x} ~ (1-p_0)^{~ (n-x)} \hspace{.2in} \mr{for} \hspace{.1in} x = 0,1,2, \ldots ,n \]](images/statug_freq0234.png)
where the variable X has a binomial distribution with parameters n and 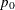 . To compute the left-sided p-value,
. To compute the left-sided p-value, 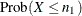 , PROC FREQ sums the binomial probabilities over x from 0 to
, PROC FREQ sums the binomial probabilities over x from 0 to 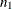 . To compute the right-sided p-value,
. To compute the right-sided p-value, 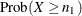 , PROC FREQ sums the binomial probabilities over x from
, PROC FREQ sums the binomial probabilities over x from 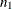 to n. The exact one-sided p-value is the minimum of the left-sided and right-sided p-values,
to n. The exact one-sided p-value is the minimum of the left-sided and right-sided p-values,
![\[ P_{1} = \min ~ ( ~ \mr{Prob}(X \leq n_1 ~ | ~ p_0 ), ~ \mr{Prob}(X \geq n_1 ~ | ~ p_0 ) ~ ) \]](images/statug_freq0238.png)
and the exact two-sided p-value is computed as 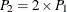 .
.
Noninferiority Test
If you specify the NONINF binomial-option, PROC FREQ provides a noninferiority test for the binomial proportion. The null hypothesis for the noninferiority test is
![\[ H_0\colon p - p_0 \leq -\delta \]](images/statug_freq0240.png)
versus the alternative
![\[ H_ a\colon p - p_0 > -\delta \]](images/statug_freq0241.png)
where  is the noninferiority margin and
is the noninferiority margin and 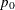 is the null proportion. Rejection of the null hypothesis indicates that the binomial proportion is not inferior to the null
value. See Chow, Shao, and Wang (2003) for more information.
is the null proportion. Rejection of the null hypothesis indicates that the binomial proportion is not inferior to the null
value. See Chow, Shao, and Wang (2003) for more information.
You can specify the value of  with the MARGIN= binomial-option, and you can specify
with the MARGIN= binomial-option, and you can specify 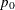 with the P= binomial-option. By default,
with the P= binomial-option. By default, 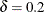 and
and 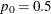 .
.
PROC FREQ provides an asymptotic Wald test for noninferiority. The test statistic is computed as
![\[ z = ( \hat{p} - p_0^\ast ) ~ / ~ \mr{se} \]](images/statug_freq0244.png)
where 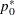 is the noninferiority limit,
is the noninferiority limit,
![\[ p_0^\ast = p_0 - \delta \]](images/statug_freq0246.png)
By default, the standard error is computed from the sample proportion as
![\[ \mr{se} = \sqrt { \hat{p} (1 - \hat{p}) / n} \]](images/statug_freq0247.png)
If you specify the VAR=NULL binomial-option, the standard error is based on the noninferiority limit (determined by the null proportion and the margin) as
![\[ \mr{se} = \sqrt { p_0^\ast (1 - p_0^\ast ) / n} \]](images/statug_freq0248.png)
If you specify the CORRECT binomial-option, PROC FREQ includes a continuity correction in the asymptotic test statistic z. The continuity correction of 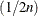 is subtracted from the numerator of the test statistic if
is subtracted from the numerator of the test statistic if 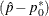 is positive; otherwise, the continuity correction is added to the numerator.
is positive; otherwise, the continuity correction is added to the numerator.
The p-value for the noninferiority test is
![\[ P_ z = \mr{Prob} ( Z > z ) \]](images/statug_freq0250.png)
where Z has a standard normal distribution.
As part of the noninferiority analysis, PROC FREQ provides asymptotic Wald confidence limits for the binomial proportion.
These confidence limits are computed as described in the section Wald Confidence Limits but use the same standard error (VAR=NULL or VAR=SAMPLE) as the noninferiority test statistic z. The confidence coefficient is 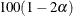 % (Schuirmann 1999). By default, if you do not specify the ALPHA= option, the noninferiority confidence limits are 90% confidence limits. You
can compare the confidence limits to the noninferiority limit,
% (Schuirmann 1999). By default, if you do not specify the ALPHA= option, the noninferiority confidence limits are 90% confidence limits. You
can compare the confidence limits to the noninferiority limit, 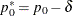 .
.
If you specify the BINOMIAL option in the EXACT statement, PROC FREQ provides an exact noninferiority test for the binomial
proportion. The exact p-value is computed by using the binomial probability function with parameters 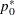 and n,
and n,
![\[ P_ x = \sum _{k=n_1}^{k=n} \binom {n}{k} (p_0^\ast )^{~ k} ~ (1-p_0^\ast )^{~ (n-k)} \]](images/statug_freq0252.png)
For more information, see Chow, Shao, and Wang (2003, p. 116). If you request exact binomial statistics, PROC FREQ also includes exact (Clopper-Pearson) confidence limits for the binomial proportion in the equivalence analysis display. For more information, see the section Exact (Clopper-Pearson) Confidence Limits.
Superiority Test
If you specify the SUP binomial-option, PROC FREQ provides a superiority test for the binomial proportion. The null hypothesis for the superiority test is
![\[ H_0\colon p - p_0 \leq \delta \]](images/statug_freq0253.png)
versus the alternative
![\[ H_ a\colon p - p_0 > \delta \]](images/statug_freq0254.png)
where  is the superiority margin and
is the superiority margin and 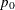 is the null proportion. Rejection of the null hypothesis indicates that the binomial proportion is superior to the null value.
You can specify the value of
is the null proportion. Rejection of the null hypothesis indicates that the binomial proportion is superior to the null value.
You can specify the value of  with the MARGIN= binomial-option, and you can specify the value of
with the MARGIN= binomial-option, and you can specify the value of 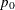 with the P= binomial-option. By default,
with the P= binomial-option. By default, 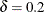 and
and 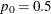 .
.
The superiority analysis is identical to the noninferiority analysis but uses a positive value of the margin  in the null hypothesis. The superiority limit equals
in the null hypothesis. The superiority limit equals 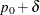 . The superiority computations follow those in the section Noninferiority Test but replace –
. The superiority computations follow those in the section Noninferiority Test but replace – with
with  . See Chow, Shao, and Wang (2003) for more information.
. See Chow, Shao, and Wang (2003) for more information.
Equivalence Test
If you specify the EQUIV binomial-option, PROC FREQ provides an equivalence test for the binomial proportion. The null hypothesis for the equivalence test is
![\[ H_0\colon p - p_0 \leq \delta _{\mi{L}} \hspace{.15in} \mr{or} \hspace{.15in} p - p_0 \geq \delta _{\mi{U}} \]](images/statug_freq0256.png)
versus the alternative
![\[ H_ a\colon \delta _{\mi{L}} < p - p_0 < \delta _{\mi{U}} \]](images/statug_freq0257.png)
where 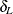 is the lower margin,
is the lower margin, 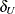 is the upper margin, and
is the upper margin, and 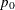 is the null proportion. Rejection of the null hypothesis indicates that the binomial proportion is equivalent to the null
value. See Chow, Shao, and Wang (2003) for more information.
is the null proportion. Rejection of the null hypothesis indicates that the binomial proportion is equivalent to the null
value. See Chow, Shao, and Wang (2003) for more information.
You can specify the value of the margins 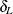 and
and 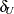 with the MARGIN= binomial-option. If you do not specify MARGIN=, PROC FREQ uses lower and upper margins of –0.2 and 0.2 by default. If you specify a single
margin value
with the MARGIN= binomial-option. If you do not specify MARGIN=, PROC FREQ uses lower and upper margins of –0.2 and 0.2 by default. If you specify a single
margin value  , PROC FREQ uses lower and upper margins of –
, PROC FREQ uses lower and upper margins of – and
and  . You can specify the null proportion
. You can specify the null proportion 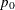 with the P= binomial-option. By default,
with the P= binomial-option. By default, 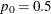 .
.
PROC FREQ computes two one-sided tests (TOST) for equivalence analysis (Schuirmann 1987). The TOST approach includes a right-sided test for the lower margin and a left-sided test for the upper margin. The overall p-value is taken to be the larger of the two p-values from the lower and upper tests.
For the lower margin, the asymptotic Wald test statistic is computed as
![\[ z_{\mi{L}} = ( \hat{p} - p_{\mi{L}}^\ast ) ~ / ~ \mr{se} \]](images/statug_freq0262.png)
where the lower equivalence limit is
![\[ p_{\mi{L}}^\ast = p_0 + \delta _{\mi{L}} \]](images/statug_freq0263.png)
By default, the standard error is computed from the sample proportion as
![\[ \mr{se} = \sqrt { \hat{p} (1 - \hat{p}) / n} \]](images/statug_freq0247.png)
If you specify the VAR=NULL binomial-option, the standard error is based on the lower equivalence limit (determined by the null proportion and the lower margin) as
![\[ \mr{se} = \sqrt { p_{\mi{L}}^\ast (1 - p_{\mi{L}}^\ast ) / n} \]](images/statug_freq0264.png)
If you specify the CORRECT binomial-option, PROC FREQ includes a continuity correction in the asymptotic test statistic 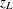 . The continuity correction of
. The continuity correction of 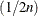 is subtracted from the numerator of the test statistic
is subtracted from the numerator of the test statistic 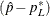 if the numerator is positive; otherwise, the continuity correction is added to the numerator.
if the numerator is positive; otherwise, the continuity correction is added to the numerator.
The p-value for the lower margin test is
![\[ P_{z,\mi{L}} = \mr{Prob} ( Z > z_{\mi{L}} ) \]](images/statug_freq0267.png)
The asymptotic test for the upper margin is computed similarly. The Wald test statistic is
![\[ z_{\mi{U}} = ( \hat{p} - p_{\mi{U}}^\ast ) ~ / ~ \mr{se} \]](images/statug_freq0268.png)
where the upper equivalence limit is
![\[ p_{\mi{U}}^\ast = p_0 + \delta _{\mi{U}} \]](images/statug_freq0269.png)
By default, the standard error is computed from the sample proportion. If you specify the VAR=NULL binomial-option, the standard error is based on the upper equivalence limit as
![\[ \mr{se} = \sqrt { p_{\mi{U}}^\ast (1 - p_{\mi{U}}^\ast ) / n} \]](images/statug_freq0270.png)
If you specify the CORRECT binomial-option, PROC FREQ includes a continuity correction of 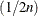 in the asymptotic test statistic
in the asymptotic test statistic 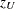 .
.
The p-value for the upper margin test is
![\[ P_{z,\mi{U}} = \mr{Prob} ( Z < z_{\mi{U}} ) \]](images/statug_freq0272.png)
Based on the two one-sided tests (TOST), the overall p-value for the test of equivalence equals the larger p-value from the lower and upper margin tests, which can be expressed as
![\[ P_ z = \max ( P_{z,\mi{L}} ~ , ~ P_{z,\mi{U}} ) \]](images/statug_freq0273.png)
As part of the equivalence analysis, PROC FREQ provides asymptotic Wald confidence limits for the binomial proportion. These
confidence limits are computed as described in the section Wald Confidence Limits, but use the same standard error (VAR=NULL or VAR=SAMPLE) as the equivalence test statistics and have a confidence coefficient
of 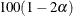 % (Schuirmann 1999). By default, if you do not specify the ALPHA= option, the equivalence confidence limits are 90% limits. If you specify VAR=NULL,
separate standard errors are computed for the lower and upper margin tests, each based on the null proportion and the corresponding
(lower or upper) margin. The confidence limits are computed by using the maximum of these two standard errors. You can compare
the confidence limits to the equivalence limits,
% (Schuirmann 1999). By default, if you do not specify the ALPHA= option, the equivalence confidence limits are 90% limits. If you specify VAR=NULL,
separate standard errors are computed for the lower and upper margin tests, each based on the null proportion and the corresponding
(lower or upper) margin. The confidence limits are computed by using the maximum of these two standard errors. You can compare
the confidence limits to the equivalence limits, 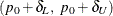 .
.
If you specify the BINOMIAL option in the EXACT statement, PROC FREQ also provides an exact equivalence test by using two
one-sided exact tests (TOST). The procedure computes lower and upper margin exact tests by using the binomial probability
function as described in the section Noninferiority Test. The overall exact p-value for the equivalence test is taken to be the larger p-value from the lower and upper margin exact tests. If you request exact statistics, PROC FREQ also includes exact (Clopper-Pearson)
confidence limits in the equivalence analysis display. The confidence coefficient is 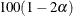 % (Schuirmann 1999). For more information, see the section Exact (Clopper-Pearson) Confidence Limits.
% (Schuirmann 1999). For more information, see the section Exact (Clopper-Pearson) Confidence Limits.
