The POWER Procedure

Analyses in the TWOSAMPLEFREQ Statement

Overview of the $2 \times 2$ Table

Notation:

   

Outcome

 
   

Failure

Success

 

Group

1

$n_1 - x_1$

$x_1$

$n_1$

 

2

$n_2 - x_2$

$x_2$

$n_2$

   

$N - m$

m

N

\begin{align*} x_1 & = \# \mbox{successes in group 1} \\ x_2 & = \# \mbox{successes in group 2} \\ m & = x_1 + x_2 = \mbox{ total }\# \mbox{successes} \\ \hat{p_1} & = \frac{x_1}{n_1} \\ \hat{p_2} & = \frac{x_2}{n_2} \\ \hat{p} & = \frac{m}{N} = w_1 \hat{p_1} + w_2 \hat{p_2} \\ \end{align*}

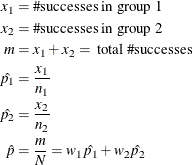
The hypotheses are

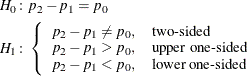
\begin{align*} H_0\colon & p_2 - p_1 = p_0 \\ H_1\colon & \left\{ \begin{array}{ll} p_2 - p_1 \ne p_0, & \mbox{two-sided} \\ p_2 - p_1 > p_0, & \mbox{upper one-sided} \\ p_2 - p_1 < p_0, & \mbox{lower one-sided} \\ \end{array} \right. \\ \end{align*}

where $p_0$ is constrained to be 0 for the likelihood ratio and Fisher’s exact tests. If $p_0 < 0$ in an upper one-sided test or $p_0 > 0$ in a lower one-sided test, then the test is a noninferiority test. If $p_0 > 0$ in an upper one-sided test or $p_0 < 0$ in a lower one-sided test, then the test is a superiority test. Although $p_0$ is unconstrained for the Pearson chi-square test, $p_0 \ne 0$ is not recommended for that test. The Farrington-Manning score test is a better choice when $p_0 \ne 0$.

Internal calculations are performed in terms of $p_1$, $p_2$, and $p_0$. An input set consisting of OR, $p_1$, and $\mr{OR}_0$ is transformed as follows:

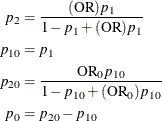
\begin{align*} p_2 & = \frac{(\mr{OR})p_1}{1-p_1+(\mr{OR})p_1} \\ p_{10} & = p_1 \\ p_{20} & = \frac{\mr{OR}_0 p_{10}}{1 - p_{10} + (\mr{OR}_0)p_{10}} \\ p_0 & = p_{20} - p_{10} \end{align*}

An input set consisting of RR, $p_1$, and $\mr{RR}_0$ is transformed as follows:

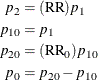
\begin{align*} p_2 & = (\mr{RR})p_1 \\ p_{10} & = p_1 \\ p_{20} & = (\mr{RR}_0)p_{10} \\ p_0 & = p_{20} - p_{10} \end{align*}

Note that the transformation of either $\mr{OR}_0$ or $\mr{RR}_0$ to $p_0$ is not unique. The chosen parameterization fixes the null value $p_{10}$ at the input value of $p_1$. Some values of $\mr{OR}_0$ or $\mr{RR}_0$ might lead to invalid values of $p_0$ ($p_0 \le 0$ or $p_0 \ge 1$), in which case an "Invalid input" error occurs.

Farrington-Manning Score Test for Two Proportions (TEST=FM)

The Farrington-Manning score test is based on equations (1), (2), and (12) in Farrington and Manning (1990). The test statistic, which is assumed to have a null distribution of $N(0,1)$ under $H_0$, is

\[ z_{FM} = \frac{\hat{p_2} - \hat{p_1} - p_0}{\left[ \frac{\tilde{p_1}(1-\tilde{p_1})}{n_1} + \frac{\tilde{p_2}(1-\tilde{p_2})}{n_2} \right]^\frac {1}{2}} \, = \, \left[ N w_1 w_2 \right]^\frac {1}{2} \frac{\hat{p_2}-\hat{p_1}- p_0}{\left[ w_2\tilde{p_1}(1-\tilde{p_1}) + w_1\tilde{p_2}(1-\tilde{p_2}) \right]^\frac {1}{2}} \]

where $\tilde{p_1}$ and $\tilde{p_2}$ are the maximum likelihood estimates of the proportions under the restriction $\tilde{p_2} - \tilde{p_1} = p_0$.

Sample size for the one-sided cases is given by equations (4) and (12) in Farrington and Manning (1990). One-sided power is computed by inverting the sample size formula. Power for the two-sided case is computed by adding the lower-sided and upper-sided powers, each evaluated at $\alpha /2$. Sample size for the two-sided case is obtained by numerically inverting the power formula,

\[ \mr{power} = \left\{ \begin{array}{ll} \Phi \left( \frac{(p_2 - p_1 - p_0) (N w_1 w_2)^\frac {1}{2} - z_{1-\alpha } \left[ w_2\tilde{p_1}(1-\tilde{p_1}) + w_1\tilde{p_2}(1-\tilde{p_2}) \right]^\frac {1}{2}}{\left[ w_2 p_1 (1 - p_1) + w_1 p_2 (1 - p_2) \right]^\frac {1}{2}} \right), & \mbox{upper one-sided} \\ \Phi \left( \frac{-(p_2 - p_1 - p_0) (N w_1 w_2)^\frac {1}{2} - z_{1-\alpha } \left[ w_2\tilde{p_1}(1-\tilde{p_1}) + w_1\tilde{p_2}(1-\tilde{p_2}) \right]^\frac {1}{2}}{\left[ w_2 p_1 (1 - p_1) + w_1 p_2 (1 - p_2) \right]^\frac {1}{2}} \right), & \mbox{lower one-sided} \\ \Phi \left( \frac{(p_2 - p_1 - p_0) (N w_1 w_2)^\frac {1}{2} - z_{1-\frac{\alpha }{2}} \left[ w_2\tilde{p_1}(1-\tilde{p_1}) + w_1\tilde{p_2}(1-\tilde{p_2}) \right]^\frac {1}{2}}{\left[ w_2 p_1 (1 - p_1) + w_1 p_2 (1 - p_2) \right]^\frac {1}{2}} \right) + \\ \quad \Phi \left( \frac{-(p_2 - p_1 - p_0) (N w_1 w_2)^\frac {1}{2} - z_{1-\frac{\alpha }{2}} \left[ w_2\tilde{p_1}(1-\tilde{p_1}) + w_1\tilde{p_2}(1-\tilde{p_2}) \right]^\frac {1}{2}}{\left[ w_2 p_1 (1 - p_1) + w_1 p_2 (1 - p_2) \right]^\frac {1}{2}} \right), & \mbox{two-sided} \\ \end{array} \right. \]

where

\begin{eqnarray*} \tilde{p}_2 & = & 2 u \cos (w) - b/(3a) \\ \tilde{p}_1 & = & \tilde{p}_2 - p_0 \\ w & = & ( \pi + \cos ^{-1}(v / u^3) ) / 3 \\ v & = & b^3 / (3a)^3 - bc/(6a^2) + d/(2a) \\ u & = & \mr{sign}(v) \sqrt {b^2 / (3a)^2 - c/(3a)} \\ a & = & 1 + w_1/w_2 \\ b & = & - \left[ 1 + w_1/w_2 + p_2 + (w_1/w_2) p_1 + p_0(w_1/w_2 + 2) \right] \\ c & = & p_0^2 + p_0 (2 p_2 + w_1/w_2 + 1) + p_2 + (w_1/w_2) p_1 \\ d & = & -p_2 p_0 (1 + p_0) \\ \end{eqnarray*}

For the one-sided cases, a closed-form inversion of the power equation yields an approximate total sample size of

\[ N = \frac{ \left[ z_{1-\alpha } \left\{ w_2\tilde{p_1}(1-\tilde{p_1}) + w_1\tilde{p_2}(1-\tilde{p_2}) \right\} ^\frac {1}{2} + z_{\mr{power}} \left\{ w_2 p_1 (1 - p_1) + w_1 p_2 (1 - p_2) \right\} ^\frac {1}{2} \right]^2 }{ w_1 w_2 (p_2 - p_1 - p_0)^2 } \]

For the two-sided case, the solution for N is obtained by numerically inverting the power equation.

Pearson Chi-Square Test for Two Proportions (TEST=PCHI)

The usual Pearson chi-square test is unconditional. The test statistic

\[ z_ P = \frac{\hat{p_2} - \hat{p_1} - p_0}{\left[ \hat{p}(1-\hat{p}) \left( \frac{1}{n_1} + \frac{1}{n_2} \right) \right]^\frac {1}{2}} \, = \, \left[ N w_1 w_2 \right]^\frac {1}{2} \frac{\hat{p_2} - \hat{p_1} - p_0}{\left[ \hat{p}(1-\hat{p}) \right]^\frac {1}{2}} \]

is assumed to have a null distribution of $N(0,1)$.

Sample size for the one-sided cases is given by equation (4) in Fleiss, Tytun, and Ury (1980). One-sided power is computed as suggested by Diegert and Diegert (1981) by inverting the sample size formula. Power for the two-sided case is computed by adding the lower-sided and upper-sided powers each evaluated at $\alpha /2$. Sample size for the two-sided case is obtained by numerically inverting the power formula. A custom null value $p_0$ for the proportion difference $p_2 - p_1$ is also supported, but it is not recommended. If you are using a non-default null value, then the Farrington-Manning score test is a better choice.

\[ \mr{power} = \left\{ \begin{array}{ll} \Phi \left( \frac{(p_2 - p_1 - p_0) (N w_1 w_2)^\frac {1}{2} - z_{1-\alpha } \left[ (w_1 p_1 + w_2 p_2) (1 - w_1 p_1 - w_2 p_2) \right]^\frac {1}{2}}{\left[ w_2 p_1 (1 - p_1) + w_1 p_2 (1 - p_2) \right]^\frac {1}{2}} \right), & \mbox{upper one-sided} \\ \Phi \left( \frac{-(p_2 - p_1 - p_0) (N w_1 w_2)^\frac {1}{2} - z_{1-\alpha } \left[ (w_1 p_1 + w_2 p_2) (1 - w_1 p_1 - w_2 p_2) \right]^\frac {1}{2}}{\left[ w_2 p_1 (1 - p_1) + w_1 p_2 (1 - p_2) \right]^\frac {1}{2}} \right), & \mbox{lower one-sided} \\ \Phi \left( \frac{(p_2 - p_1 - p_0) (N w_1 w_2)^\frac {1}{2} - z_{1-\frac{\alpha }{2}} \left[ (w_1 p_1 + w_2 p_2) (1 - w_1 p_1 - w_2 p_2) \right]^\frac {1}{2}}{\left[ w_2 p_1 (1 - p_1) + w_1 p_2 (1 - p_2) \right]^\frac {1}{2}} \right) + \\ \quad \Phi \left( \frac{-(p_2 - p_1 - p_0) (N w_1 w_2)^\frac {1}{2} - z_{1-\frac{\alpha }{2}} \left[ (w_1 p_1 + w_2 p_2) (1 - w_1 p_1 - w_2 p_2) \right]^\frac {1}{2}}{\left[ w_2 p_1 (1 - p_1) + w_1 p_2 (1 - p_2) \right]^\frac {1}{2}} \right), & \mbox{two-sided} \\ \end{array} \right. \]

For the one-sided cases, a closed-form inversion of the power equation yields an approximate total sample size

\[ N = \frac{ \left[ z_{1-\alpha } \left\{ (w_1 p_1 + w_2 p_2) (1 - w_1 p_1 - w_2 p_2) \right\} ^\frac {1}{2} + z_{\mr{power}} \left\{ w_2 p_1 (1 - p_1) + w_1 p_2 (1 - p_2) \right\} ^\frac {1}{2} \right]^2 }{ w_1 w_2 (p_2 - p_1 - p_0)^2 } \]

For the two-sided case, the solution for N is obtained by numerically inverting the power equation.

Likelihood Ratio Chi-Square Test for Two Proportions (TEST=LRCHI)

The usual likelihood ratio chi-square test is unconditional. The test statistic

\[ z_{\mr{LR}} = (-1_{\{ p_2 < p_1\} })\sqrt {2N \sum _{i=1}^2 \left[ w_ i \hat{p_ i} \log \left( \frac{\hat{p_ i}}{\hat{p}} \right) + w_ i (1-\hat{p_ i}) \log \left( \frac{1-\hat{p_ i}}{1-\hat{p}} \right) \right]} \]

is assumed to have a null distribution of $N(0,1)$ and an alternative distribution of $N(\delta ,1)$, where

\[ \delta = N^\frac {1}{2} (-1_{\{ p_2 < p_1\} })\sqrt {2 \sum _{i=1}^2 \left[ w_ i p_ i \log \left( \frac{p_ i}{w_1 p_1 + w_2 p_2} \right) + w_ i (1-p_ i) \log \left( \frac{1-p_ i}{1-(w_1 p_1 + w_2 p_2)} \right) \right]} \]

The approximate power is

\[ \mr{power} = \left\{ \begin{array}{ll} \Phi \left( \delta - z_{1-\alpha } \right), & \mbox{upper one-sided} \\ \Phi \left( - \delta - z_{1-\alpha } \right), & \mbox{lower one-sided} \\ \Phi \left( \delta - z_{1-\frac{\alpha }{2}} \right) + \Phi \left( - \delta - z_{1-\frac{\alpha }{2}} \right), & \mbox{two-sided} \\ \end{array} \right. \\ \]

For the one-sided cases, a closed-form inversion of the power equation yield an approximate total sample size

\[ N = \left( \frac{z_{\mr{power}} + z_{1-\alpha }}{\delta } \right)^2 \]

For the two-sided case, the solution for N is obtained by numerically inverting the power equation.

Fisher’s Exact Conditional Test for Two Proportions (Test=FISHER)

Fisher’s exact test is conditional on the observed total number of successes m. Power and sample size computations are based on a test with similar power properties, the continuity-adjusted arcsine test. The test statistic

\begin{align*} z_ A & = (4N w_1 w_2)^\frac {1}{2} \left[ \mr{arcsin}\left( \left[ \hat{p_2} + \frac{1}{2N w_2} (1_{\{ \hat{p_2} < \hat{p_1}\} } - 1_{\{ \hat{p_2} > \hat{p_1}\} }) \right]^\frac {1}{2} \right) \right. \\ & \quad \left. - \mr{arcsin}\left( \left[ \hat{p_1} + \frac{1}{2N w_1} (1_{\{ \hat{p_1} < \hat{p_2}\} } - 1_{\{ \hat{p_1} > \hat{p_2}\} }) \right]^\frac {1}{2} \right) \right] \end{align*}

is assumed to have a null distribution of $N(0,1)$ and an alternative distribution of $N(\delta ,1)$, where

\begin{align*} \delta & = (4N w_1 w_2)^\frac {1}{2} \left[ \mr{arcsin}\left( \left[ p_2 + \frac{1}{2N w_2} (1_{\{ p_2 < p_1\} } - 1_{\{ p_2 > p_1\} }) \right]^\frac {1}{2} \right) \right. \\ & \quad \left. - \mr{arcsin}\left( \left[ p_1 + \frac{1}{2N w_1} (1_{\{ p_1 < p_2\} } - 1_{\{ p_1 > p_2\} }) \right]^\frac {1}{2} \right) \right] \end{align*}

The approximate power for the one-sided balanced case is given by Walters (1979) and is easily extended to the unbalanced and two-sided cases:

\[ \mr{power} = \left\{ \begin{array}{ll} \Phi \left( \delta - z_{1-\alpha } \right), & \mbox{upper one-sided} \\ \Phi \left( - \delta - z_{1-\alpha } \right), & \mbox{lower one-sided} \\ \Phi \left( \delta - z_{1-\frac{\alpha }{2}} \right) + \Phi \left( - \delta - z_{1-\frac{\alpha }{2}} \right), & \mbox{two-sided} \\ \end{array} \right. \\ \]

The approximation is valid only for $N \ge 1/(2 w_1 w_2 |p_1 - p_2|)$.