The GLIMMIX Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function -
Details
 Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance (Sandwich) EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance (Sandwich) EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics -
Examples
 Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey Data
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey Data - References
In a generalized linear model, the log likelihood is well defined, and an objective function for estimation of the parameters is simple to construct based on the independence of the data. In a GLMM, several problems must be overcome before an objective function can be computed.
-
The model might be vacuous in the sense that no valid joint distribution can be constructed either in general or for a particular set of parameter values. For example, if
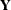 is an equicorrelated
is an equicorrelated 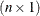 vector of binary responses with the same success probability and a symmetric distribution, then the lower bound on the correlation
parameter depends on n and
vector of binary responses with the same success probability and a symmetric distribution, then the lower bound on the correlation
parameter depends on n and  (Gilliland and Schabenberger, 2001). If further restrictions are placed on the joint distribution, as in Bahadur (1961), the correlation is also restricted from above.
(Gilliland and Schabenberger, 2001). If further restrictions are placed on the joint distribution, as in Bahadur (1961), the correlation is also restricted from above.
-
The dependency between mean and variance for nonnormal data places constraints on the possible correlation models that simultaneously yield valid joint distributions and a desired conditional distributions. Thus, for example, aspiring for conditional Poisson variates that are marginally correlated according to a spherical spatial process might not be possible.
-
Even if the joint distribution is feasible mathematically, it still can be out of reach computationally. When data are independent, conditional on the random effects, the marginal log likelihood can in principle be constructed by integrating out the random effects from the joint distribution. However, numerical integration is practical only when the number of random effects is small and when the data have a clustered (subject) structure.
Because of these special features of generalized linear mixed models, many estimation methods have been put forth in the literature. The two basic approaches are (1) to approximate the objective function and (2) to approximate the model. Algorithms in the second category can be expressed in terms of Taylor series (linearizations) and are hence also known as linearization methods. They employ expansions to approximate the model by one based on pseudo-data with fewer nonlinear components. The process of computing the linear approximation must be repeated several times until some criterion indicates lack of further progress. Schabenberger and Gregoire (1996) list numerous algorithms based on Taylor series for the case of clustered data alone. The fitting methods based on linearizations are usually doubly iterative. The generalized linear mixed model is approximated by a linear mixed model based on current values of the covariance parameter estimates. The resulting linear mixed model is then fit, which is itself an iterative process. On convergence, the new parameter estimates are used to update the linearization, which results in a new linear mixed model. The process stops when parameter estimates between successive linear mixed model fits change only within a specified tolerance.
Integral approximation methods approximate the log likelihood of the GLMM and submit the approximated function to numerical optimization. Various techniques are used to compute the approximation: Laplace methods, quadrature methods, Monte Carlo integration, and Markov chain Monte Carlo methods. The advantage of integral approximation methods is to provide an actual objective function for optimization. This enables you to perform likelihood ratio tests among nested models and to compute likelihood-based fit statistics. The estimation process is singly iterative. The disadvantage of integral approximation methods is the difficulty of accommodating crossed random effects and multiple subject effects, and the inability to accommodate R-side covariance structures, even only R-side overdispersion. The number of random effects should be small for integral approximation methods to be practically feasible.
The advantages of linearization-based methods include a relatively simple form of the linearized model that typically can be fit based on only the mean and variance in the linearized form. Models for which the joint distribution is difficult—or impossible—to ascertain can be fit with linearization-based approaches. Models with correlated errors, a large number of random effects, crossed random effects, and multiple types of subjects are thus excellent candidates for linearization methods. The disadvantages of this approach include the absence of a true objective function for the overall optimization process and potentially biased estimates, especially for binary data when the number of observations per subject is small (see the section Notes on Bias of Estimators for further comments and considerations about the bias of estimates in generalized linear mixed models). Because the objective function to be optimized after each linearization update depends on the current pseudo-data, objective functions are not comparable across linearizations. The estimation process can fail at both levels of the double iteration scheme.
By default the GLIMMIX procedure fits generalized linear mixed models based on linearizations. The default estimation method in GLIMMIX for models containing random effects is a technique known as restricted pseudo-likelihood (RPL) (Wolfinger and O’Connell, 1993) estimation with an expansion around the current estimate of the best linear unbiased predictors of the random effects (METHOD=RSPL).
Two maximum likelihood estimation methods based on integral approximation are available in the GLIMMIX procedure. If you choose METHOD=LAPLACE in a GLMM, the GLIMMIX procedure performs maximum likelihood estimation based on a Laplace approximation of the marginal log likelihood. See the section Maximum Likelihood Estimation Based on Laplace Approximation for details about the Laplace approximation with PROC GLIMMIX. If you choose METHOD=QUAD in the PROC GLIMMIX statement in a generalized linear mixed model, the GLIMMIX procedure estimates the model parameters by adaptive Gauss-Hermite quadrature. See the section Maximum Likelihood Estimation Based on Adaptive Quadrature for details about the adaptive Gauss-Hermite quadrature approximation with PROC GLIMMIX.
The following subsections discuss the three estimation methods in turn. Keep in mind that your modeling possibilities are increasingly restricted in the order of these subsections. For example, in the class of generalized linear mixed models, the pseudo-likelihood estimation methods place no restrictions on the covariance structure, and Laplace estimation adds restriction with respect to the R-side covariance structure. Adaptive quadrature estimation further requires a clustered data structure—that is, the data must be processed by subjects.
Table 43.22: Model Restrictions Depending on Estimation Method
|
Method |
Restriction |
|---|---|
|
RSPL, RMPL |
None |
|
MSPL, MMPL |
None |
|
LAPLACE |
No R-side effects |
|
QUAD |
No R-side effects |
|
Requires SUBJECT= effect |
|
|
Requires processing by subjects |