Nonlinear Mixed Model :: SAS/STAT(R) 12.3 User's Guide

Nonlinear Mixed Model

In a nonlinear mixed model (NLMM), the fixed and/or random effects enter the conditional mean function nonlinearly. If the mean function is a general, nonlinear function, then it is customary to assume that the conditional distribution is normal, such as in modeling growth curves or pharmacokinetic response. This is not a requirement, however. An example of a nonlinear mixed model is the following logistic growth curve model for the jth observation of the ith subject (cluster):

$\displaystyle f(\bbeta ,\bgamma _ i,x_{ij}) =$	$\displaystyle \frac{\beta _1 + \gamma _{i1}}{1 + \exp [-(x_{ij} - \beta _2)/ (\beta _3 + \gamma _{i2})]}$
$\displaystyle Y_{ij} =$	$\displaystyle f(\bbeta ,\bgamma _ i,x_{ij}) + \epsilon _{ij}$
$\displaystyle \left[\begin{array}{c}\gamma _{i1}\cr \gamma _{i2}\end{array}\right] \sim$	$\displaystyle N\left( \left[\begin{array}{c}0\cr 0\end{array}\right], \left[\begin{array}{cc} \sigma ^2_1 & \sigma _{12} \cr \sigma _{21} & \sigma ^2_2 \end{array}\right] \right)$
$\displaystyle Y_{ij}\|\gamma _{i1},\gamma _{i2} \sim$	$\displaystyle N(0,\sigma ^2_\epsilon )$

The inclusion of R-side covariance structures in GLMM and NLMM models is not as straightforward as in linear mixed models for the following reasons:

The normality of the conditional distribution in the LMM enables straightforward modeling of the covariance structure because the mean structure and covariance structure are not functionally related.
The linearity of the random effects in the LMM leads to a marginal distribution that incorporates the 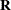$\bR$ matrix in a natural and meaningful way.

To incorporate R-side covariance structures when random effects enter nonlinearly or when the data are not normally distributed requires estimation approaches that rely on linearizations of the mixed model. Among such estimation methods are the pseudo-likelihood methods that are available with the GLIMMIX procedure. Generalized estimating equations also solve this marginal estimation problem for nonnormal data; these are available with the GENMOD procedure.