The GLIMMIX Procedure

Confidence Bounds Based on Likelihoods

Families of statistical tests can be inverted to produce confidence limits for parameters. The confidence region for parameter $\theta$ is the set of values for which the corresponding test fails to reject $H\colon \theta =\theta _0$ . When parameters are estimated by maximum likelihood or a likelihood-based technique, it is natural to consider the likelihood ratio test statistic for H in the test inversion. When there are multiple parameters in the model, however, you need to supply values for these nuisance parameters during the test inversion as well.

In the following, suppose that $\btheta$ is the covariance parameter vector and that one of its elements, $\theta$ , is the parameter of interest for which you want to construct a confidence interval. The other elements of $\btheta$ are collected in the nuisance parameter vector $\btheta _2$ . Suppose that $\widehat{\btheta }$ is the estimate of $\btheta$ from the overall optimization and that $L(\widehat{\btheta })$ is the likelihood evaluated at that estimate. If estimation is based on pseudo-data, then $L(\widehat{\btheta })$ is the pseudo-likelihood based on the final pseudo-data. If estimation uses a residual (restricted) likelihood, then L denotes the restricted maximum likelihood and $\widehat{\btheta }$ is the REML estimate.

Profile Likelihood Bounds

The likelihood ratio test statistic for testing $H\colon \theta =\theta _0$ is

$2 \left\{ \log \left\{ L(\widehat{\btheta })\right\} - \log \left\{ L(\theta _0,\widehat{\btheta }_2)\right\} \right\}$

where $\widehat{\btheta }_2$ is the likelihood estimate of $\btheta _2$ under the restriction that $\theta = \theta _0$ . To invert this test, a function is defined that returns the maximum likelihood for a fixed value of $\theta$ by seeking the maximum over the remaining parameters. This function is termed the profile likelihood (Pawitan, 2001, Ch. 3.4),

$\lambda _ p = L(\btheta _2|\widetilde{\theta }) = \sup _{\btheta _2} L(\widetilde{\theta },\btheta _2)$

In computing $\lambda _ p$ , $\theta$ is fixed at $\widetilde{\theta }$ and $\btheta _2$ is estimated. In mixed models, this step typically requires a separate, iterative optimization to find the estimate of $\btheta _2$ while $\theta$ is held fixed. The $(1-\alpha )\times 100\%$ profile likelihood confidence interval for $\theta$ is then defined as the set of values for $\widetilde{\theta }$ that satisfy

$2 \left\{ \log \left\{ L(\widehat{\btheta })\right\} - \log \left\{ L(\btheta _2|\widetilde{\theta }) \right\} \right\} \leq \chi ^2_{1,(1-\alpha )}$

The GLIMMIX procedure seeks the values $\widetilde{\theta }_ l$ and $\widetilde{\theta }_ u$ that mark the endpoints of the set around $\widehat{\theta }$ that satisfy the inequality. The values $(\widetilde{\theta }_ l$ and $\widetilde{\theta }_ u)$ are then called the $(1-\alpha )\times 100\%$ confidence bounds for $\theta$ . Note that the GLIMMIX procedure assumes that the confidence region is not disjoint and relies on the convexity of $L(\widehat{\btheta })$ .

It is not always possible to find values $\widetilde{\theta }_ l$ and $\widetilde{\theta }_ u$ that satisfy the inequalities. For example, when the parameter space is ( $0,\infty )$ and

$2 \left\{ \log \left\{ L(\widehat{\btheta })\right\} - \log \left\{ L(\btheta _2 | 0) \right\} \right\} > \chi ^2_{1,(1-\alpha )}$

a lower bound cannot be found at the desired confidence level. The GLIMMIX procedure reports the right-tail probabilities that are achieved by the underlying likelihood ratio statistic separately for lower and upper bounds.

Effect of Scale Parameter

When a scale parameter $\phi$ is eliminated from the optimization by profiling from the likelihood, some parameters might be expressed as ratios with $\phi$ in the optimization. This is the case, for example, in variance component models. The profile likelihood confidence bounds are reported on the scale of the parameter in the overall optimization. In case parameters are expressed as ratios with $\phi$ or functions of $\phi$ , the column RatioEstimate is added to the “Covariance Parameter Estimates” table. If parameters are expressed as ratios with $\phi$ and you want confidence bounds for the unscaled parameter, you can prevent profiling of $\phi$ from the optimization with the NOPROFILE option in the PROC GLIMMIX statement, or choose estimated likelihood confidence bounds with the TYPE=ELR suboption of the CL option in the COVTEST statement. Note that the NOPROFILE option is automatically in effect with METHOD=LAPLACE and METHOD=QUAD.

Estimated Likelihood Bounds

Computing profile likelihood ratio confidence bounds can be computationally expensive, because of the need to repeatedly estimate $\btheta _2$ in a constrained optimization. A computationally simpler method to construct confidence bounds from likelihood-based quantities is to use the estimated likelihood (Pawitan, 2001, Ch. 10.7) instead of the profile likelihood. An estimated likelihood technique replaces the nuisance parameters in the test inversion with some other estimate. If you choose the TYPE=ELR suboption of the CL option in the COVTEST statement, the GLIMMIX procedure holds the nuisance parameters fixed at the likelihood estimates. The estimated likelihood statistic for inversion is then

$\lambda _ e = L(\widetilde{\theta },\widehat{\btheta }_2)$

where $\widehat{\btheta }_2$ are the elements of $\widehat{\btheta }$ that correspond to the nuisance parameters. As the values of $\widetilde{\theta }$ are varied, no reestimation of $\btheta _2$ takes place. Although computationally more economical, estimated likelihood intervals do not take into account the variability associated with the nuisance parameters. Their coverage can be satisfactory if the parameter of interest is not (or only weakly) correlated with the nuisance parameters. Estimated likelihood ratio intervals can fall short of the nominal coverage otherwise.

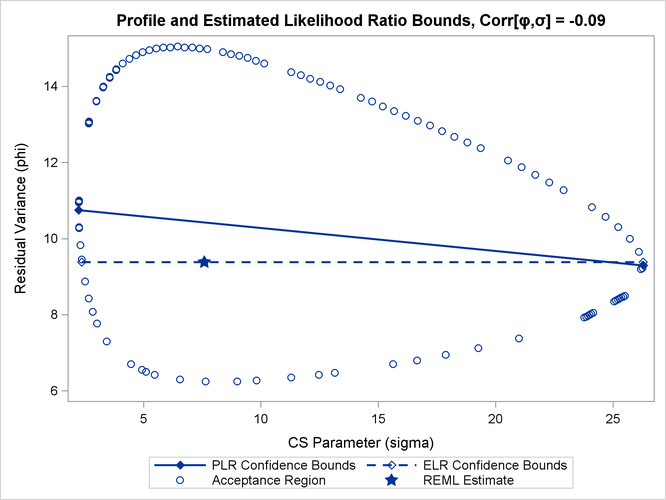
Figure 41.11 depicts profile and estimated likelihood ratio intervals for the parameter $\sigma$ in a two-parameter compound-symmetric model, $\btheta = [\sigma ,\phi ]’$ , in which the correlation between the covariance parameters is small. The elliptical shape traces the set of values for which the likelihood ratio test rejects the hypothesis of equality with the solution. The interior of the ellipse is the “acceptance” region of the test. The solid and dashed lines depict the PLR and ELR confidence limits for $\sigma$ , respectively. Note that both confidence limits intersect the ellipse and that the ELR interval passes through the REML estimate of $\phi$ . The PLR bounds are found as those points intersecting the ellipse, where $\phi$ equals the constrained REML estimate.

Figure 41.11: PLR and ELR Intervals, Small Correlation between Parameters

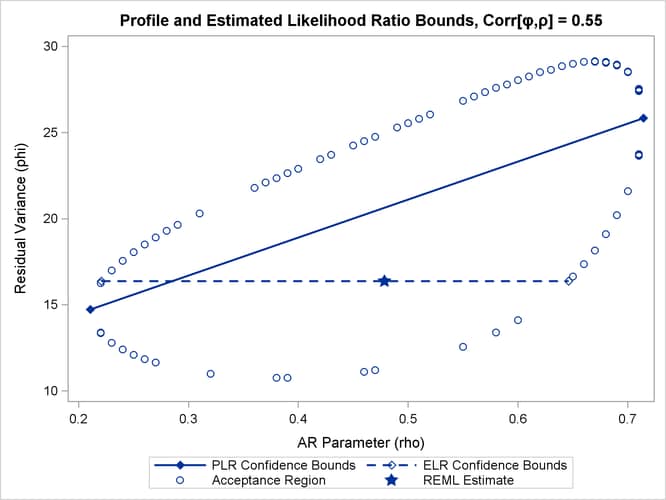
The major axes of the ellipse in Figure 41.11 are nearly aligned with the major axes of the coordinate system. As a consequence, the line connecting the PLR bounds passes close to the REML estimate in the full model. As a result, ELR bounds will be similar to PLR bounds. Figure 41.12 displays a different scenario, a two-parameter AR(1) covariance structure with a more substantial correlation between the AR(1) parameter ( $\rho$ ) and the residual variance ( $\phi$ ).

Figure 41.12: PLR and ELR Intervals, Large Correlation between Parameters

The correlation between the parameters yields an acceptance region whose major axes are not aligned with the axes of the coordinate system. The ELR bound for $\rho$ passes through the REML estimate of $\phi$ from the full model and is much shorter than the PLR interval. The PLR interval aligns with the major axis of the acceptance region; it is the preferred confidence interval.