The GLIMMIX Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function -
Details
 Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance (Sandwich) EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance (Sandwich) EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics -
Examples
 Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary Data
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary Data - References
The likelihood ratio test (LRT) compares the likelihoods of two models where parameter estimates are obtained in two parameter
spaces, the space ![]() and the restricted subspace
and the restricted subspace ![]() . In the GLIMMIX procedure, the full model defines
. In the GLIMMIX procedure, the full model defines ![]() and the test-specification in the COVTEST statement determines the null parameter space
and the test-specification in the COVTEST statement determines the null parameter space ![]() . The likelihood ratio procedure consists of the following steps (see, for example, Bickel and Doksum 1977, p. 210):
. The likelihood ratio procedure consists of the following steps (see, for example, Bickel and Doksum 1977, p. 210):
-
Find the estimate
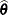 of
of 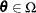 . Compute the likelihood
. Compute the likelihood 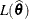 .
.
-
Find the estimate
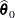 of
of 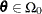 . Compute the likelihood
. Compute the likelihood 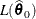 .
.
-
Form the likelihood ratio
![\[ \overline{\lambda } = \frac{L(\widehat{\btheta })}{L(\widehat{\btheta }_0)} \]](images/statug_glimmix0775.png)
-
Find a function
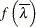 that has a known distribution.
that has a known distribution. 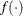 serves as the test statistic for the likelihood ratio test.
serves as the test statistic for the likelihood ratio test.
Please note the following regarding the implementation of these steps in the COVTEST statement of the GLIMMIX procedure.
-
The function
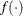 in step 4 is always taken to be
in step 4 is always taken to be
![\[ \lambda = 2 \log \left\{ \overline{\lambda } \right\} \]](images/statug_glimmix0778.png)
which is twice the difference between the log likelihoods for the full model and the model under the COVTEST restriction.
-
For METHOD=RSPL and METHOD=RMPL, the test statistic is based on the restricted likelihood.
-
For GLMMs involving pseudo-data, the test statistics are based on the pseudo-likelihood or the restricted pseudo-likelihood and are based on the final pseudo-data.
-
The parameter space
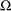 for the full model is typically not an unrestricted space. The GLIMMIX procedure imposes boundary constraints for variance
components and scale parameters, for example. The specification of the subspace
for the full model is typically not an unrestricted space. The GLIMMIX procedure imposes boundary constraints for variance
components and scale parameters, for example. The specification of the subspace 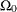 must be consistent with these full-model constraints; otherwise the test statistic
must be consistent with these full-model constraints; otherwise the test statistic 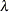 does not have the needed distribution. You can remove the boundary restrictions with the NOBOUND option in the PROC GLIMMIX statement or the NOBOUND option in the PARMS statement.
does not have the needed distribution. You can remove the boundary restrictions with the NOBOUND option in the PROC GLIMMIX statement or the NOBOUND option in the PARMS statement.