| Unconditional Simulation |
It is a simple matter to produce an  random number, and by stacking
random number, and by stacking  such numbers in a column vector you obtain a vector with independent standard normal components
such numbers in a column vector you obtain a vector with independent standard normal components  . The meaning of the terms independence and randomness in the context of a deterministic algorithm required for the generation of these numbers is somewhat subtle; see Knuth (1973, Vol. 2, Chapter 3) for a discussion of these issues.
. The meaning of the terms independence and randomness in the context of a deterministic algorithm required for the generation of these numbers is somewhat subtle; see Knuth (1973, Vol. 2, Chapter 3) for a discussion of these issues.
Rather than  , what is required is the generation of a vector
, what is required is the generation of a vector 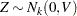 —that is,
—that is,
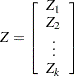 |
with covariance matrix
 |
where
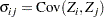 |
If the covariance matrix is symmetric and positive definite, it has a Cholesky root 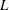 such that
such that  can be factored as
can be factored as
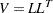 |
where 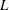 is lower triangular. See Ralston and Rabinowitz (1978, Chapter 9, Section 3-3) for details. This vector
is lower triangular. See Ralston and Rabinowitz (1978, Chapter 9, Section 3-3) for details. This vector 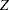 can be generated by the transformation
can be generated by the transformation  . Note that this is where the assumption of multivariate normality is crucial. If
. Note that this is where the assumption of multivariate normality is crucial. If 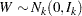 , then
, then  is also normal or Gaussian. The mean of
is also normal or Gaussian. The mean of 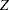 is
is
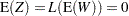 |
and the variance is
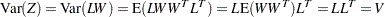 |
Finally, let 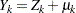 ; that is, you add a mean term to each variable
; that is, you add a mean term to each variable 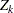 . The covariance structure of the
. The covariance structure of the  remains the same. Unconditional simulation is done by simply repeatedly generating
remains the same. Unconditional simulation is done by simply repeatedly generating 
 random numbers, stacking them, and performing the transformation
random numbers, stacking them, and performing the transformation
 |