The SIM2D Procedure

Simulating a Subregion for Economic Feasibility

The coal seam must be of a minimum thickness, called a cutoff value, for a mining operation to be profitable. Suppose that, for a subregion of the measured area, the cost of mining is higher than in the remaining areas due to the geology of the overburden. This higher cost results in a higher thickness cutoff value for the subregion. Suppose also that it is determined from a detailed cost analysis that at least 60% of the subregion must exceed a seam thickness of 39.7 feet for profitability.

How can you use the SRF model (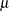 and ) and 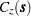the measured seam thickness values 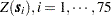, to determine, in some approximate way, whether at least 60% of the subregion exceeds this minimum?

Spatial prediction does not appear to be helpful in answering this question. Although it is easy to determine whether a predicted value at a location in the subregion is above the 39.7-feet cutoff value, it is not clear how to incorporate the standard error associated with the predicted value. The standard error is what characterizes the stochastic nature of the prediction (and the underlying SRF). It is clear that it must be included in any realistic approach to the problem.

A conditional simulation, on the other hand, seems to be a natural way of obtaining an approximate answer. By simulating the SRF on a sufficiently fine grid in the subregion, you can determine the proportion of grid points in which the mean value over realizations exceeds the 39.7-feet cutoff and compare it with the 60% value needed for profitability.

It is desirable in any simulation study that the quantity being estimated (in this case, the proportion that exceeds the 39.7-feet cutoff) not depend on the number of simulations performed. For example, suppose that the maximum seam thickness is simulated. It is likely that the maximum value increases as the number of simulations performed increases. Hence, a simulation is not useful for such an estimate. A simulation is useful for determining the distribution of the maximum, but there are general theoretical results for such distributions, making such a simulation unnecessary. See Leadbetter, Lindgren, and Rootzen (1983) for details.

In the case of simulating the proportion that exceeds the 39.7-feet cutoff, it is expected that this quantity will settle down to a fixed value as the number of realizations increases. At a fixed grid point, the quantity being compared with the cutoff value is the mean over all simulated realizations; this mean value settles down to a fixed number as the number of realizations increases. In the same manner, the proportion of the grid where the mean values exceed the cutoff also becomes constant. This can be tested using PROC SIM2D.

A crucial, nonprovable assumption in applying SRF theory to the coal seam thickness data is that the values 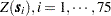, represent a single realization from the set of all possible realizations consistent with the SRF model ( 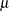and 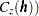. A conditional simulation repeatedly produces other possible simulated realizations consistent with the model and data. However, the only concern of the mining company is this single unique realization. It is not concerned about similar coal fields to be mined sometime in the future; it might never see another coal field remotely similar to this one, or it might not be in business in the future.

Hence the proportion found by generating repeated simulated realizations must somehow relate back to the unique realization that is the coal field (seam thickness). This is done by interpreting the proportion found from a simulation to the spatial mean proportion for the unique realization. The term "spatial mean" is simply an appropriate integral over the fixed (but unknown) spatial function 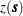. (The SRF is denoted 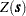; a particular realization, a deterministic function of the spatial coordinates, is denoted .)

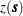This interpretation requires an ergodic assumption, which is also needed in the original estimation of 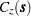. See Cressie (1993, pp. 53–58) for a discussion of ergodicity and Gaussian SRFs.