The NPAR1WAY Procedure
Tests Based on the Empirical Distribution Function
If you specify the EDF option, PROC NPAR1WAY computes tests based on the empirical distribution function. These include the Kolmogorov-Smirnov and Cramer-von Mises tests, and also the Kuiper test for two-sample data. This section gives formulas for these test statistics. For further information about the formulas and the interpretation of EDF statistics, see Hollander and Wolfe (1999) and Gibbons and Chakraborti (1992). For details about the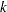 
-sample analogs of the Kolmogorov-Smirnov and Cramer-von Mises statistics, see Kiefer (1959).
The empirical distribution function (EDF) of a sample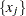 
, 
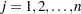, is defined as
 |
where 
is an indicator function. PROC NPAR1WAY uses the subsample of values within the 
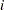th class level to generate an EDF for the class, 
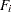. The EDF for the overall sample, pooled over classes, can also be expressed as
 |
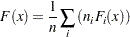where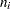 
is the number of observations in the 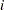th class level, and 
is the total number of observations.
Kolmogorov-Smirnov Test
The Kolmogorov-Smirnov statistic measures the maximum deviation of the EDF within the classes from the pooled EDF. PROC NPAR1WAY computes the Kolmogorov-Smirnov statistic as
 |
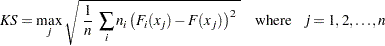The asymptotic Kolmogorov-Smirnov statistic is computed as
 |
For each class level 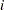and overall, PROC NPAR1WAY displays the value of 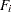at the maximum deviation from 
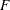and the value 
at the maximum deviation from 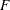. PROC NPAR1WAY also gives the observation where the maximum deviation occurs.
If there are only two class levels, PROC NPAR1WAY computes the two-sample Kolmogorov-Smirnov test statistic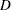 
as
 |
The p-value for this test is the probability that 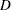is greater than the observed value 
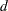under the null hypothesis of no difference between class levels (samples). PROC NPAR1WAY computes the asymptotic p-value for 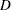with the approximation
 |
where
 |
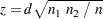The quality of this approximation has been studied by Hodges (1957).
If you specify the D option, or if you request exact Kolmogorov-Smirnov p-values with the KS option in the EXACT statement, PROC NPAR1WAY also computes the one-sided Kolmogorov-Smirnov statistics 
and 
for two-sample data as
 |
 |
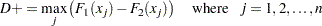The asymptotic probability that is greater than the observed value 
, under the null hypothesis of no difference between the two class levels, is computed as
 |
Similarly, the asymptotic probability that is greater than the observed value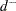 
is computed as
 |
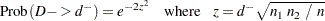To request exact p-values for the Kolmogorov-Smirnov statistics, you can specify the KS option in the EXACT statement. See the section Exact Tests for more information.
Cramer-von Mises Test
The Cramer-von Mises statistic is defined as
 |
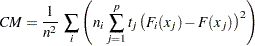where 
is the number of ties at the 
th distinct value and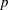 
is the number of distinct values. The asymptotic value is computed as
 |
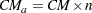PROC NPAR1WAY displays the contribution of each class level to the sum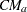 
.
Kuiper Test
For data with two class levels, PROC NPAR1WAY computes the Kuiper statistic, its scaled value for the asymptotic distribution, and the asymptotic p-value. The Kuiper statistic is computed as
 |
The asymptotic value is
 |
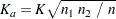PROC NPAR1WAY displays the value of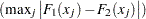 
for each class level.
The p-value for the Kuiper test is the probability of observing a larger value of 
under the null hypothesis of no difference between the two classes. PROC NPAR1WAY computes this p-value according to Owen (1962, p. 441).