Introduction to Regression Procedures: Generalized Additive Models: The GAM Procedure

Generalized Additive Models: The GAM Procedure

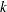Generalized additive models are nonparametric models in which one or more regressor variables are present and can make different smooth contributions to the mean function. For example, if $\text{[math]}$ is a vector of $\text{[math]}$ regressor for the 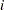$\text{[math]}$ th observation, then an additive model represents the mean function as

$\text{[math]}$

The individual functions 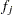$\text{[math]}$ can have a parametric or nonparametric form. If all 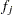$\text{[math]}$ are parametric, the GAM procedure fits a fully parametric model. If some 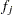$\text{[math]}$ are nonparametric, the GAM procedure fits a semiparametric model. Otherwise, the models are fully nonparametric.

The generalization of additive models is akin to the generalization for linear models: nonnormal data are accommodated by explicitly modeling the distribution of the data as a member of the exponential family and by applying a monotonic link function that provides a mapping between the predictor and the mean of the data.