Introduction to Statistical Modeling with SAS/STAT Software: Maximum Likelihood Estimation

Maximum Likelihood Estimation

To estimate the parameters in a linear model with mean function 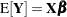$\text{[math]}$ by maximum likelihood, you need to specify the distribution of the response vector 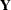$\text{[math]}$ . In the linear model with a continuous response variable, it is commonly assumed that the response is normally distributed. In that case, the estimation problem is completely defined by specifying the mean and variance of 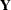$\text{[math]}$ in addition to the normality assumption. The model can be written as 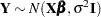$\text{[math]}$ , where the notation 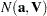$\text{[math]}$ indicates a multivariate normal distribution with mean vector $\text{[math]}$ and variance matrix 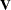$\text{[math]}$ . The log likelihood for 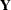$\text{[math]}$ then can be written as

$\text{[math]}$

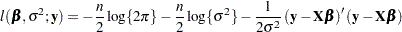This function is maximized in 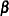$\text{[math]}$ when the sum of squares 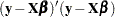$\text{[math]}$ is minimized. The maximum likelihood estimator of 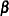$\text{[math]}$ is thus identical to the ordinary least squares estimator. To maximize 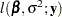$\text{[math]}$ with respect to 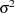$\text{[math]}$ , note that

$\text{[math]}$

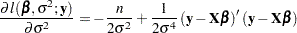Hence the MLE of 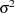$\text{[math]}$ is the estimator

	$\text{[math]}$	$\text{[math]}$
	$\text{[math]}$	$\text{[math]}$

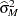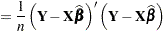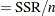This is a biased estimator of 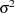$\text{[math]}$ , with a bias that decreases with $\text{[math]}$ .