Reduction notation can be used to represent differences in sums of squares (SS) for two models. The notation 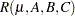denotes the complete main-effects model for effects 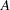, , 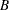and 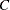. The notation

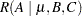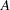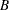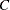denotes the difference between the model SS for the complete main-effects model containing , , and and the model SS for the reduced model containing only 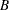and .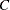

In other words, this notation represents the differences in model SS produced by

proc glm;
   class a b c;
   model y = a b c;
run;

and

proc glm;
   class b c;
   model y = b c;
run;

As another example, consider a regression equation with four independent variables. The notation 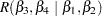denotes the differences in model SS between

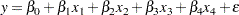and

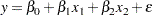This is the difference in the model SS for the models produced, respectively, by

model y = x1 x2 x3 x4;

and

model y = x1 x2;

The following examples demonstrate the ability to manipulate the symbolic representation of a generating set. Note that any operations performed on the symbolic notation have corresponding row operations that are performed on the generating set itself.