| The HPMIXED Procedure |
| Computing and Maximizing the Likelihood |
In computing the restricted likelihood function given previously, the determinants of the matrices 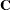 and
and 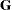 can be obtained effectively by using Cholesky decomposition. The quadratic term
can be obtained effectively by using Cholesky decomposition. The quadratic term 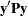 can be expressed in terms of solutions of mixed model equations as follows:
can be expressed in terms of solutions of mixed model equations as follows:
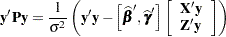 |
By default, the HPMIXED procedure profiles out the residual variance  from the parameter vector
from the parameter vector 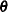 . Let
. Let 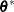 be the new parameter vector such that
be the new parameter vector such that 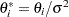 . The profiled objective function becomes
. The profiled objective function becomes
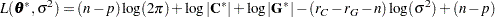 |
where 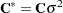 and
and  are the profiled versions of
are the profiled versions of 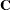 and
and 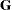 ,
, 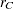 and
and 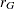 are the ranks of
are the ranks of 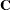 and
and 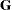 . Minimizing analytically for
. Minimizing analytically for  yields
yields
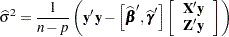 |
Optimizing the likelihood calls for derivatives with respect to the parameters. The first and second derivatives of the log-likelihood function 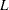 with respect to scalar variance components
with respect to scalar variance components 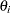 and
and 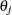 are
are
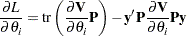 |
and
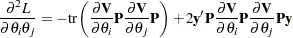 |
The default quasi-Newton method of optimization for the HPMIXED procedure requires only first derivatives of the log likelihood, and these are readily derived by solving the mixed model equations. For example, when  , the first derivative of the log likelihood with respect to the parameter
, the first derivative of the log likelihood with respect to the parameter  can be computed as follows:
can be computed as follows:
 |
where  is the size of
is the size of  vector and
vector and 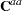 is the part of the
is the part of the 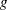 -inverse of the mixed model equation coefficient matrix
-inverse of the mixed model equation coefficient matrix 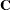 corresponding to the random effect
corresponding to the random effect  .
.
The second derivative of the log likelihood needs to be computed only if you specify certain nondefault optimization techniques in the NLOPTIONS statement, namely TECH=NEWRAP, TECH=NRRIDG, or TECH=TRUREG; see NLOPTIONS Statement in Chapter 19, Shared Concepts and Topics, for more information about optimization techniques. For these second-derivative-based optimization techniques, the HPMIXED procedure does not actually use the true second derivative matrix, or observed information matrix, as defined earlier. Instead, it uses an alternative matrix that is more efficient to compute for large problems and that can be more stable. This alternative is called the average information matrix, and it is defined as follows. The expected value of the second derivative is
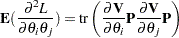 |
It is this trace that is computationally inefficient to evaluate. But if you average the expected information matrix defined by this formula with the observed information matrix defined by the preceding formula for the true second derivative, then the trace term cancels, leaving just a quadratic expression in 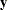 . This quadratic expression defines the average information (Johnson and Thompson; 1995) with respect to
. This quadratic expression defines the average information (Johnson and Thompson; 1995) with respect to 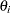 and
and 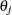 :
:
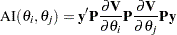 |
Copyright © SAS Institute, Inc. All Rights Reserved.