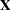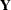Let represent the design matrix and the 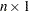vector of dependent variables. (See the section Parameterization of PROC GLM Models for information about how 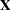is formed from your model specification.)

The normal equations are solved using a modified sweep routine that produces a generalized inverse 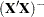and a solution 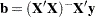. The modification is that rows and columns corresponding to diagonal elements that are found during sweeping to be zero (or within the expected level of numerical error of zero) are zeroed out. The 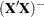produced by this procedure satisfies the following two equations:

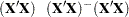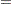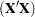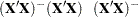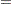Pringle and Rayner (1971) call a generalized inverse with these characteristics a -inverse, and this is the term usually used in SAS documentation and output. Urquardt (1968) uses the term reflexive -inverse to emphasize that 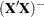is a generalized inverse of 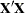in the same way that 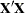is a generalized inverse of 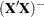. Note that a -inverse is not necessarily unique: if 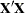is singular, then sweeping the matrix in a different order will result in a different -inverse that also satisfies the two preceding equations.

For each effect in the model, a matrix 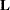is computed such that the rows of 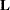are estimable. Tests of the hypothesis are then made by first computing

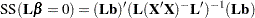and then computing the associated 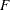value by using the mean squared error.