| The SIM2D Procedure |
| Introduction to Spatial Simulation |
The purpose of spatial simulation is to produce a set of partial realizations of a spatial random field (SRF)  in a way that preserves a specified mean
in a way that preserves a specified mean  and covariance structure
and covariance structure  . The realizations are partial in the sense that they occur only at a finite set of locations
. The realizations are partial in the sense that they occur only at a finite set of locations  . These locations are typically on a regular grid, but they can be arbitrary locations in the plane.
. These locations are typically on a regular grid, but they can be arbitrary locations in the plane.
PROC SIM2D produces simulations for continuous processes in two dimensions by using the lower-upper (LU) decomposition method. In these simulations the possible values of the measured quantity  at location
at location  can vary continuously over a certain range. An additional assumption, needed for computational purposes, is that the spatial random field
can vary continuously over a certain range. An additional assumption, needed for computational purposes, is that the spatial random field 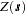 is Gaussian. The section Details: SIM2D Procedure provides more information about different types of spatial simulation and associated computational methods.
is Gaussian. The section Details: SIM2D Procedure provides more information about different types of spatial simulation and associated computational methods.
Spatial simulation is different from spatial prediction, where the emphasis is on predicting a point value at a given grid location. In this sense, spatial prediction is local. In contrast, spatial simulation is global; the emphasis is on the entire realization  .
.
Given the correct mean 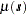 and covariance structure
and covariance structure  , SRF quantities that are difficult or impossible to calculate in a spatial prediction context can easily be approximated by functions of multiple simulations.
, SRF quantities that are difficult or impossible to calculate in a spatial prediction context can easily be approximated by functions of multiple simulations.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.