Algorithm

Least trimmed squares (LTS) regression is based on the subset of observations (out of a total of observations) whose least squares fit possesses the smallest sum of squared residuals. The coverage can be set between and . The LTS method was proposed by Rousseeuw (1984, p. 876) as a highly robust regression estimator with breakdown value . The ROBUSTREG procedure uses the FAST-LTS algorithm given by Rousseeuw and Van Driessen (2000). The intercept adjustment technique is also used in this implementation. However, because this adjustment is expensive to compute, it is optional. You can use the IADJUST option in the PROC statement to request or suppress the intercept adjustment. By default, PROC ROBUSTREG does intercept adjustment for data sets with fewer than 10000 observations. The steps of the algorithm are described briefly as follows. Refer to Rousseeuw and Van Driessen (2000) for details.

1. The default is , where is the number of independent variables. You can specify any integer with with the H= option in the MODEL statement. The breakdown value for LTS, , is reported. The default is a good compromise between breakdown value and statistical efficiency.

2. If (single regressor), the procedure uses the exact algorithm of Rousseeuw and Leroy (1987, p. 172).

3. If , the procedure uses the following algorithm. If , where is the size of the subgroups (you can specify by using the SUBGROUPSIZE= option in the PROC statement; by default, ), draw a random -subset and compute the regression coefficients by using these points (if the regression is degenerate, draw another -subset). Compute the absolute residuals for all observations in the data set, and select the first points with smallest absolute residuals. From this selected -subset, carry out C-steps (Concentration step; see Rousseeuw and Van Driessen (2000) for details. You can specify with the CSTEP= option in the PROC statement; by default, ). Redraw -subsets and repeat the preceding computing procedure times, and then find the (at most) solutions with the lowest sums of squared residuals. can be specified with the NREP= option in the PROC statement. By default, NREP=. For small and , all subsets are used and the NREP= option is ignored (Rousseeuw and Hubert 1996). can be specified with the NBEST= option in the PROC statement. By default, NBEST=10. For each of these best solutions, take C-steps until convergence and find the best final solution.

4. If , construct 5 disjoint random subgroups with size . If , the data are split into at most four subgroups with or more observations in each subgroup, so that each observation belongs to a subgroup and the subgroups have roughly the same size. Let denote the number of subgroups. Inside each subgroup, repeat the procedure in step 3 times and keep the best solutions. Pool the subgroups, yielding the merged set of size . In the merged set, for each of the best solutions, carry out C-steps by using and and keep the best solutions. In the full data set, for each of these best solutions, take C-steps by using and until convergence and find the best final solution.

The robust version of for the LTS estimate is defined as

for models with the intercept term and as

for models without the intercept term, where

is a preliminary estimate of the parameter in the distribution function .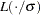

Here is chosen to make consistent, assuming a Gaussian model. Specifically,

with 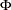and being the distribution function and the density function of the standard normal distribution, respectively.

Final Weighted Scale Estimator

The ROBUSTREG procedure displays two scale estimators, and Wscale. The estimator Wscale is a more efficient scale estimator based on the preliminary estimate , and it is defined as

where

You can specify with the CUTOFF= option in the MODEL statement. By default, .

Algorithm

The ROBUSTREG procedure implements the algorithm by Marazzi (1993) for the S estimate, which is a refined version of the algorithm proposed by Ruppert (1992). The refined algorithm is briefly described as follows.

Initialize .

1. Draw a random -subset of the total observations and compute the regression coefficients by using these observations (if the regression is degenerate, draw another -subset), where can be specified with the SUBSIZE= option. By default, .

2. Compute the residuals: for . If , set ; if , set ;
   while , set ; go to step 3.
   If and , go to step 3; otherwise, go to step 5.

3. Solve for the equation

   using an iterative algorithm.

4. If and , go to step 5. Otherwise, set and . If , return and ; otherwise, go to step 5.

5. If , set and return to step 1; otherwise, return and .

The ROBUSTREG procedure does the following refinement step by default. You can request that this refinement not be done by using the NOREFINE option in the PROC statement.

1. Let . Using the values and from the previous steps, compute M estimates and of and with the setup for M estimation in the section M Estimation. If , give a warning and return and ; otherwise, return and .

You can specify with the TOLERANCE= option; by default, TOLERANCE=0.001. Alternately, you can specify with the NREP= option. You can also use the options NREP=NREP0 or NREP=NREP1 to determine according to the following table. NREP=NREP0 is set as the default.

and Deviance

The robust version of for the S estimate is defined as

for the model with the intercept term and

for the model without the intercept term, where is the S estimate of the scale in the full model, is the S estimate of the scale in the regression model with only the intercept term, and is the S estimate of the scale without any regressor. The deviance is defined as the optimal value of the objective function on the scale:

Asymptotic Covariance and Confidence Intervals

Since the S estimate satisfies the first-order necessary conditions as the M estimate, it has the same asymptotic covariance as that of the M estimate. All three estimators of the asymptotic covariance for the M estimate in the section Asymptotic Covariance and Confidence Intervals can be used for the S estimate. Besides, the weighted covariance estimator H4 described in the section Asymptotic Covariance and Confidence Intervals is also available and is set as the default. Confidence intervals for estimated parameters are computed from the diagonal elements of the estimated asymptotic covariance matrix.