| The PHREG Procedure |
Testing Linear Hypotheses about Regression Coefficients
Linear hypotheses for 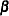 are expressed in matrix form as
are expressed in matrix form as
 |
where L is a matrix of coefficients for the linear hypotheses, and c is a vector of constants. The Wald chi-square statistic for testing 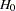 is computed as
is computed as
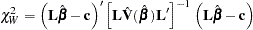 |
where 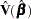 is the estimated covariance matrix. Under
is the estimated covariance matrix. Under 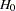 ,
, 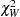 has an asymptotic chi-square distribution with r degrees of freedom, where r is the rank of
has an asymptotic chi-square distribution with r degrees of freedom, where r is the rank of  .
.
Optimal Weights for the AVERAGE option in the TEST Statement
Let 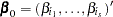 , where
, where 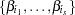 is a subset of
is a subset of  regression coefficients. For any vector
regression coefficients. For any vector 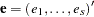 of length
of length  ,
,
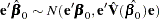 |
To find  such that
such that 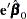 has the minimum variance, it is necessary to minimize
has the minimum variance, it is necessary to minimize 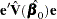 subject to
subject to 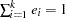 . Let
. Let 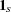 be a vector of 1’s of length
be a vector of 1’s of length  . The expression to be minimized is
. The expression to be minimized is
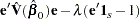 |
where 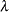 is the Lagrange multipler. Differentiating with respect to
is the Lagrange multipler. Differentiating with respect to  and
and 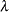 , respectively, yields
, respectively, yields
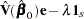 |
 |
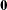 |
|||
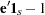 |
 |
 |
Solving these equations gives
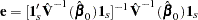 |
This provides a one degree-of-freedom test for testing the null hypothesis 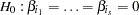 with normal test statistic
with normal test statistic
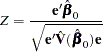 |
This test is more sensitive than the multivariate test specified by the TEST statement
Multivariate: test X1, ..., Xs;
where X , ..., X
, ..., X are the variables with regression coefficients
are the variables with regression coefficients 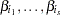 , respectively.
, respectively.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.