| The MIANALYZE Procedure |
| Multivariate Inferences |
Multivariate inference based on Wald tests can be done with 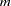 imputed data sets. The approach is a generalization of the approach taken in the univariate case (Rubin 1987, p. 137; Schafer 1997, p. 113). Suppose that
imputed data sets. The approach is a generalization of the approach taken in the univariate case (Rubin 1987, p. 137; Schafer 1997, p. 113). Suppose that  and
and 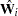 are the point and covariance matrix estimates for a
are the point and covariance matrix estimates for a  -dimensional parameter
-dimensional parameter 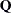 (such as a multivariate mean) from the
(such as a multivariate mean) from the  imputed data set,
imputed data set,  = 1, 2, ...,
= 1, 2, ..., 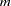 . Then the combined point estimate for
. Then the combined point estimate for 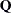 from the multiple imputation is the average of the
from the multiple imputation is the average of the 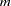 complete-data estimates:
complete-data estimates:
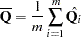 |
Suppose that  is the within-imputation covariance matrix, which is the average of the
is the within-imputation covariance matrix, which is the average of the 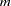 complete-data estimates:
complete-data estimates:
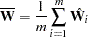 |
And suppose that 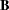 is the between-imputation covariance matrix:
is the between-imputation covariance matrix:
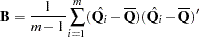 |
Then the covariance matrix associated with  is the total covariance matrix
is the total covariance matrix
 |
The natural multivariate extension of the  statistic used in the univariate case is the
statistic used in the univariate case is the 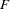 statistic
statistic
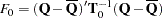 |
with degrees of freedom  and
and
 |
where
 |
is an average relative increase in variance due to nonresponse (Rubin 1987, p. 137; Schafer 1997, p. 114).
However, the reference distribution of the statistic 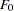 is not easily derived. Especially for small
is not easily derived. Especially for small 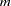 , the between-imputation covariance matrix
, the between-imputation covariance matrix 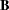 is unstable and does not have full rank for
is unstable and does not have full rank for 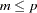 (Schafer 1997, p. 113).
(Schafer 1997, p. 113).
One solution is to make an additional assumption that the population between-imputation and within-imputation covariance matrices are proportional to each other (Schafer 1997, p. 113). This assumption implies that the fractions of missing information for all components of 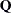 are equal. Under this assumption, a more stable estimate of the total covariance matrix is
are equal. Under this assumption, a more stable estimate of the total covariance matrix is
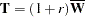 |
With the total covariance matrix 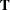 , the
, the 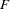 statistic (Rubin 1987, p. 137)
statistic (Rubin 1987, p. 137)
 |
has an 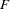 distribution with degrees of freedom
distribution with degrees of freedom  and
and 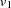 , where
, where
 |
For  , PROC MIANALYZE uses the degrees of freedom
, PROC MIANALYZE uses the degrees of freedom 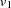 in the analysis. For
in the analysis. For 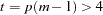 , PROC MIANALYZE uses
, PROC MIANALYZE uses 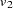 , a better approximation of the degrees of freedom given by Li, Raghunathan, and Rubin (1991):
, a better approximation of the degrees of freedom given by Li, Raghunathan, and Rubin (1991):
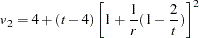 |
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.