If you use events/trials MODEL syntax, each observation is split into two observations. One has response value 1 with a frequency equal to the frequency of the original observation (which is 1 if the FREQ statement is not used) times the value of the events variable. The other observation has response value 2 and a frequency equal to the frequency of the original observation times the value of (trials–events). These two observations will have the same explanatory variable values and the same FREQ and WEIGHT values as the original observation.

For either single-trial or events/trials syntax, let 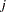index all observations. In other words, for single-trial syntax, 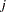indexes the actual observations. And, for events/trials syntax, 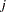indexes the observations after splitting (as described in the preceding paragraph). If your data set has 30 observations and you use single-trial syntax, 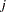has values from 1 to 30; if you use events/trials syntax, 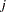has values from 1 to 60.

Suppose the response variable in a cumulative response model can take on the ordered values 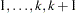, where 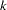is an integer . The likelihood for the 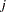th observation with ordered response value 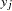and explanatory variables vector is given by

where 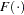is the logistic, normal, or extreme-value distribution function, 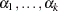are ordered intercept parameters, and is the common slope parameter vector.

For the generalized logit model, letting the 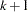st level be the reference level, the intercepts 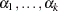are unordered and the slope vector 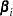varies with each logit. The likelihood for the 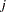th observation with response value 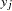and explanatory variables vector is given by