Product-Limit Method

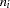Let represent the distinct event times. For each , let be the number of surviving units, the size of the risk set, just prior to 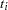. Let be the number of units that fail at 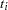, and let .

The product-limit estimate of the SDF at 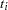is the cumulative product

Notice that the estimator is defined to be right continuous; that is, the events at 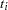are included in the estimate of . The corresponding estimate of the standard error is computed using Greenwood’s formula (Kalbfleisch and Prentice; 1980) as

The first quartile (or the 25th percentile) of the survival time is the time beyond which 75% of the subjects in the population under study are expected to survive. It is estimated by

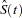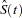If is exactly equal to 0.75 from to , the first quartile is taken to be . If it happens that is greater than 0.75 for all values of t, the first quartile cannot be estimated and is represented by a missing value in the printed output.

The general formula for estimating the th percentile point is

The second quartile (the median) and the third quartile of survival times correspond to p=0.5 and p=0.75, respectively.

Brookmeyer and Crowley (1982) have constructed the confidence interval for the median survival time based on the confidence interval for the 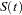. The methodology is generalized to construct the confidence interval for the th percentile based on a -transformed confidence interval for 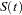(Klein and Moeschberger; 1997). You can use the CONFTYPE= option to specify the -transformation. The 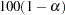% confidence interval for the first quantile survival time is the set of all points that satisfy

where is the first derivative of and 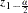is the th percentile of the standard normal distribution.

Consider the bone marrow transplant data described in Example 49.2. The following table illustrates the construction of the confidence limits for the first quartile in the ALL group. Values of that lie between = 1.965 are highlighted.

Consider the LINEAR transformation where . The event times that satisfy include 107, 109, 110, 122, 129, 172, 192, 194, and 230. The confidence of the interval [107, 230] is less than 95%. Brookmeyer and Crowley (1982) suggest extending the confidence interval to but not including the next event time. As such the 95% confidence interval for the first quartile based on the linear transform is [107, 276). The following table lists the confidence intervals for the various transforms.

Sometimes, the confidence limits for the quartiles cannot be estimated. For convenience of explanation, consider the linear transform . If the curve representing the upper confidence limits for the survivor function lies above 0.75, the upper confidence limit for first quartile cannot be estimated. On the other hand, if the curve representing the lower confidence limits for the survivor function lies above 0.75, the lower confidence limit for the quartile cannot be estimated.

The estimated mean survival time is

where 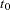is defined to be zero. When the largest observed time is censored, this sum underestimates the mean. The standard error of is estimated as

where

If the largest observed time is not an event, you can use the TIMELIM= option to specify a time limit and estimate the mean survival time limited to the time and its standard error by replacing 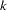by with .

Nelson-Aalen Estimate of the Cumulative Hazard Function

The Nelson-Aalen cumulative hazard estimator, defined up to the largest observed time on study, is

and its estimated variance is