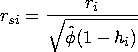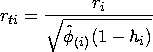Standardized and Studentized Residuals

Fit Analyses

Standardized and Studentized Residuals

For linear models, the variance of the residual r_i is

$\rm{Var}( r_{i}) = {\sigma}^2 (1- h_{i})$

and an estimate of the standard error of the residual is

$\rm{STDERR}( r_{i}) = s \sqrt{1- h_{i}}$

Thus, the residuals can be modified to better detect unusual observations. The ratio of the residual to its standard error, called the standardized residual, is

$r_{si} = \frac{r_{i}}{s \sqrt{1- h_{i}} }$

If the residual is standardized with an independent estimate of ${\sigma}^2$ , the result has a Student's t distribution if the data satisfy the normality assumption. If you estimate ${\sigma}^2$ by s²_(i), the estimate of ${\sigma}^2$ obtained after deleting the ith observation, the result is a studentized residual:

$r_{ti} = \frac{r_{i}}{s_{(i)} \sqrt{1- h_{i}} }$

Observations with | r_ti|>2 may deserve investigation.

For generalized linear models, the standardized and studentized residuals are

$r_{si} = \frac{r_{i}}{\sqrt{\hat{ \phi} (1- h_{i})}}$

$r_{ti} = \frac{r_{i}}{\sqrt{ \hat{ \phi}_{(i)} (1- h_{i})}}$

where ${\hat{ \phi}}$ is the estimate of the dispersion parameter $\phi$ ,and ${ \hat{ \phi}_{(i)}}$ is a one-step approximation of $\phi$ after excluding the ith observation.

The standardized residuals are stored in variables named RS_yname and the Studentized residuals are stored in variables named RT_yname for each response variable, where yname is the response variable name.

Top of Page