The SHEWHART Procedure
Displaying Trends in Process Data
Note: See X-Bar Chart for Data with Nonlinear Trend in the SAS/QC Sample Library.
Time trends due to tool wear, environmental changes, and other gradual process changes are sometimes observed in 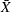 charts. The presence of a systematic trend makes it difficult to interpret the chart because the control limits are designed
to indicate expected variation strictly due to common causes.
charts. The presence of a systematic trend makes it difficult to interpret the chart because the control limits are designed
to indicate expected variation strictly due to common causes.
You can use the REG procedure (or other modeling procedure) in conjunction with the SHEWHART procedure to determine whether
a process with a time trend is in control. With the REG procedure, you can model the trend and save the fitted subgroup means
 and the residual subgroup means
and the residual subgroup means  in an output data set. Then, using this data as input to the SHEWHART procedure, you can create a trend chart, which displays a trend plot of the fitted subgroup means together with an
in an output data set. Then, using this data as input to the SHEWHART procedure, you can create a trend chart, which displays a trend plot of the fitted subgroup means together with an 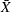 chart for the residual subgroup means, thus removing the time-dependent component of the data from its random component.
Having accounted for the time trend, you can decide whether the process is in control by examining the
chart for the residual subgroup means, thus removing the time-dependent component of the data from its random component.
Having accounted for the time trend, you can decide whether the process is in control by examining the 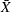 chart.
chart.
The following example illustrates the steps used to create a trend chart for a SAS data set named toolwear that contains diameter measurements for 20 subgroup samples each consisting of eight parts:
data toolwear;
input hour @;
do i=1 to 8;
input Diameter @;
output;
end;
drop i;
datalines;
1 10.0434 9.9427 9.9548 9.8056
10.0780 10.0302 10.1173 10.0215
2 10.1976 9.9654 10.0425 10.1183
10.0963 10.1635 10.1382 10.1265
3 10.0552 10.0695 10.2495 10.1753
10.1268 10.1229 10.1351 10.2084
4 10.1600 10.1378 10.2433 10.2634
10.1808 10.1601 10.1035 10.0027
5 9.9611 10.4322 10.1066 10.2653
10.0310 10.1409 10.2709 10.0585
6 10.2208 10.2298 10.2427 10.2315
10.2048 10.2824 10.3347 10.1650
7 10.2670 10.3793 10.2539 10.4037
10.3281 10.1327 10.1986 10.1841
8 10.2537 10.1981 10.2935 10.4308
10.3195 10.3122 10.2033 10.3220
9 10.2488 10.1866 10.3678 10.1755
10.3225 10.2375 10.2466 10.3387
10 10.3744 10.5221 10.2890 10.3123
10.5134 10.3212 10.3139 10.1565
11 10.3525 10.3237 10.4605 10.5139
10.3650 10.1171 10.3863 10.2061
12 10.3279 10.3338 10.1885 10.2810
10.2400 10.3617 10.2938 10.2656
13 10.1651 10.2404 10.1814 10.2330
10.3094 10.3373 10.3266 10.3830
14 10.3554 10.4577 10.5435 10.4805
10.5358 10.4631 10.3689 10.1750
15 10.2962 10.4221 10.3578 10.4694
10.3465 10.4499 10.4645 10.3986
16 10.6002 10.1924 10.3437 10.3228
10.3438 10.3503 10.3761 10.3137
17 10.4015 10.3592 10.3187 10.4108
10.4834 10.4807 10.2178 10.3897
18 10.4514 10.4492 10.3373 10.4497
10.4197 10.3496 10.3949 10.1585
19 10.3445 10.3310 10.4472 10.4684
10.3975 10.2714 10.2952 10.6255
20 10.2612 10.3824 10.4240 10.3120
10.5744 10.4204 10.4073 10.3783
;