Functions

Deriving Control Chart Constants

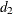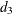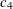You can use the functions D2, D3, and C4 to calculate standard control chart constants that are derived from $d_2$ , $d_3$ and $c_4$ . For reference, the following equations for some of these constants are provided:

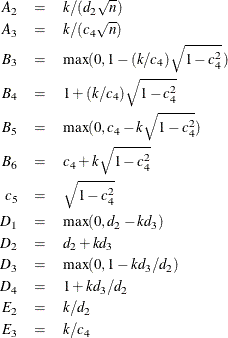
$\begin{eqnarray*} A_2 & = & k/(d_2 \sqrt {n}) \\ A_3 & = & k/(c_4 \sqrt {n}) \\ B_3 & = & \max (0,1-(k/c_4) \sqrt {1-c_4^2}\: ) \\ B_4 & = & 1+(k/c_4) \sqrt {1-c_4^2} \\ B_5 & = & \max (0,c_4-k\sqrt {1-c_4^2}) \\ B_6 & = & c_4+k \sqrt {1-c_4^2} \\ c_5 & = & \sqrt {1-c_4^2} \\ D_1 & = & \max (0,d_2-kd_3) \\ D_2 & = & d_2+kd_3 \\ D_3 & = & \max (0,1-kd_3/d_2) \\ D_4 & = & 1+kd_3/d_2 \\ E_2 & = & k/d_2 \\ E_3 & = & k/c_4 \end{eqnarray*}$

In the preceding equations, k is the multiple of standard error (k = 3 in the case of 3 $\sigma$ limits), and n is the subgroup sample size. The use of these control chart constants is discussed in the American Society for Quality Control (1983), the American Society for Testing and Materials (1976), Montgomery (1996), and Wadsworth, Stephens, and Godfrey (1986).

Although you do not ordinarily need to calculate control chart constants when using the SHEWHART procedure, you may find the D2, D3, and C4 functions useful for creating LIMITS= data sets that contain control limits to be read by the SHEWHART procedure.